machine learning review
Linear regression
Introduction
什么是回归?
- 根据给定的特征,预测感兴趣变量的值
- 数学角度:回归旨在学习一个函数\(f(\cdot)\),该函数能够对输入数据\(x\)与输出值\(y\)之间的关系进行建模。
线性回归:就是限制这个函数只能为线性的形式
代价/损失函数:
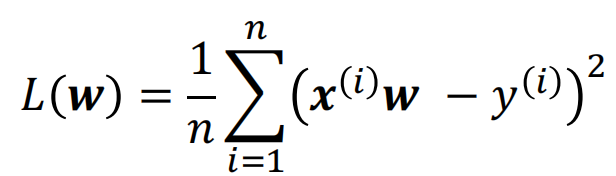
或者
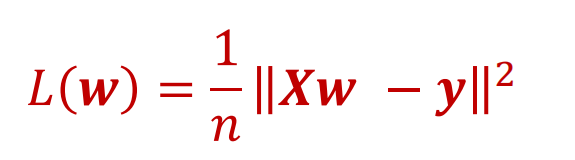
close-form的解决方法并不总是存在,或者代价太高,因此产生了梯度下降法。
梯度下降: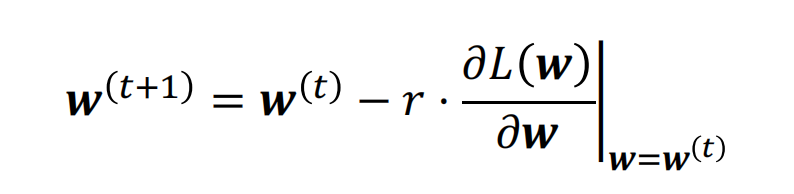
学习率的设置:
- 如果学习率太小:收敛的速度会很慢
- 如果学习率太大:迭代可能会发散
随机梯度下降:
- 梯度下降:每次迭代需要计算训练集里的所有数据样本,对于大数据集来说复杂度太高,为解决这样的问题我们可以选用数据集的一小部分:mini-batch
- 获取小批量的方法:
- reshuffling
- Segmenting
随机梯度是平均梯度的无偏估计:

其他的优化方法
牛顿法
- 优势:
- 不需要人为的选择学习率
- 更快的收敛速度
- 劣势:
- 计算更加昂贵
- 优势:
拟牛顿法
共轭梯度法
坐标下降法
- 普遍收敛更加,但是计算更加昂贵
Logistic regression
在分类任务中,目标变量的值应该在0-1之间,线性回归的输出值与分类任务不兼容
可以通过Sigmod函数将线性回归转换为逻辑回归,如下:
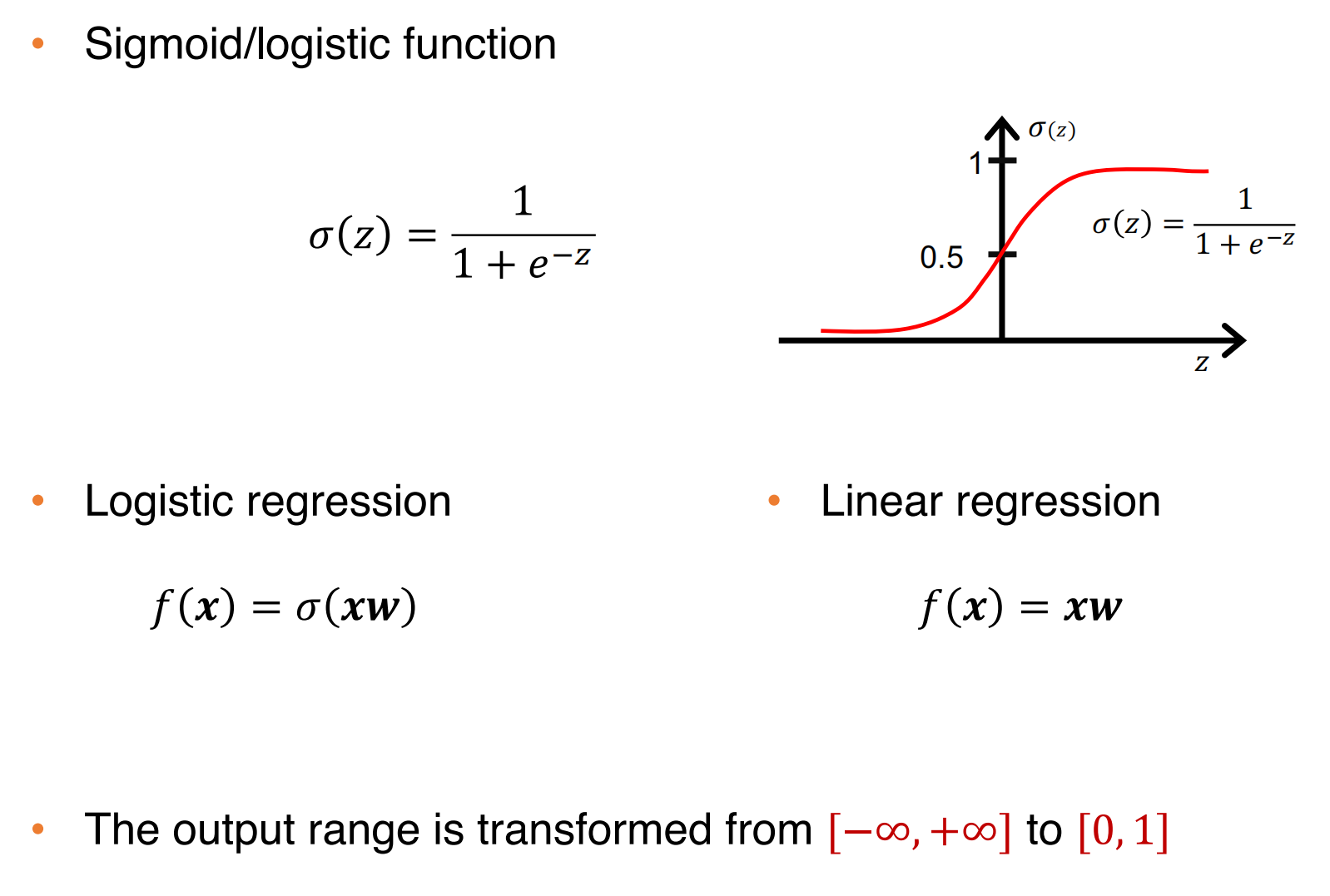
cross-entropy loss交叉熵损失:
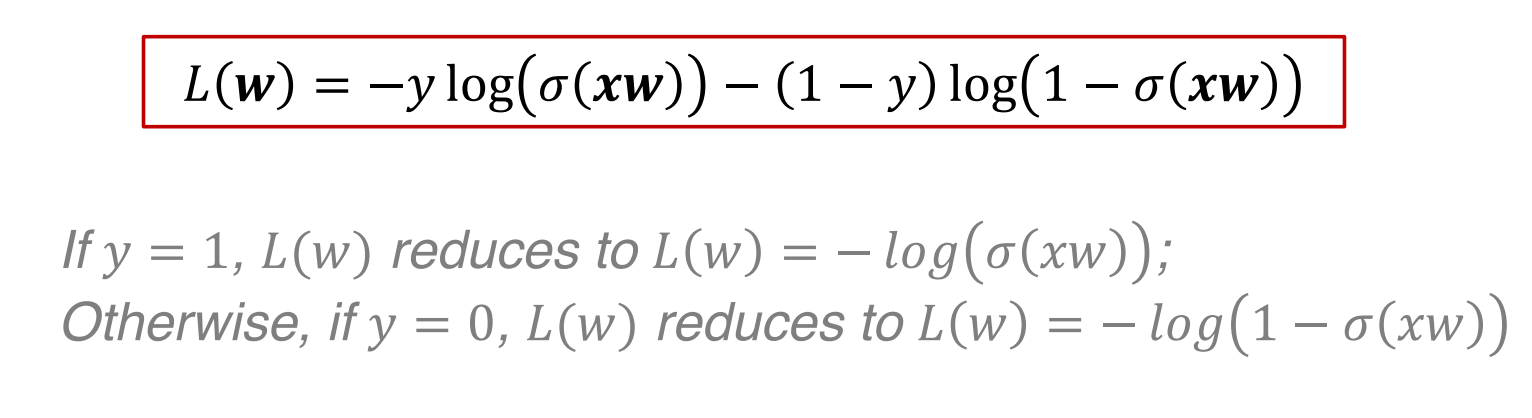
取对数:一是防止下溢,二是使连乘变成连加
多分类case
处理多分类情况:
- one-to-all:为每种类别都训练一个分类器,如下:
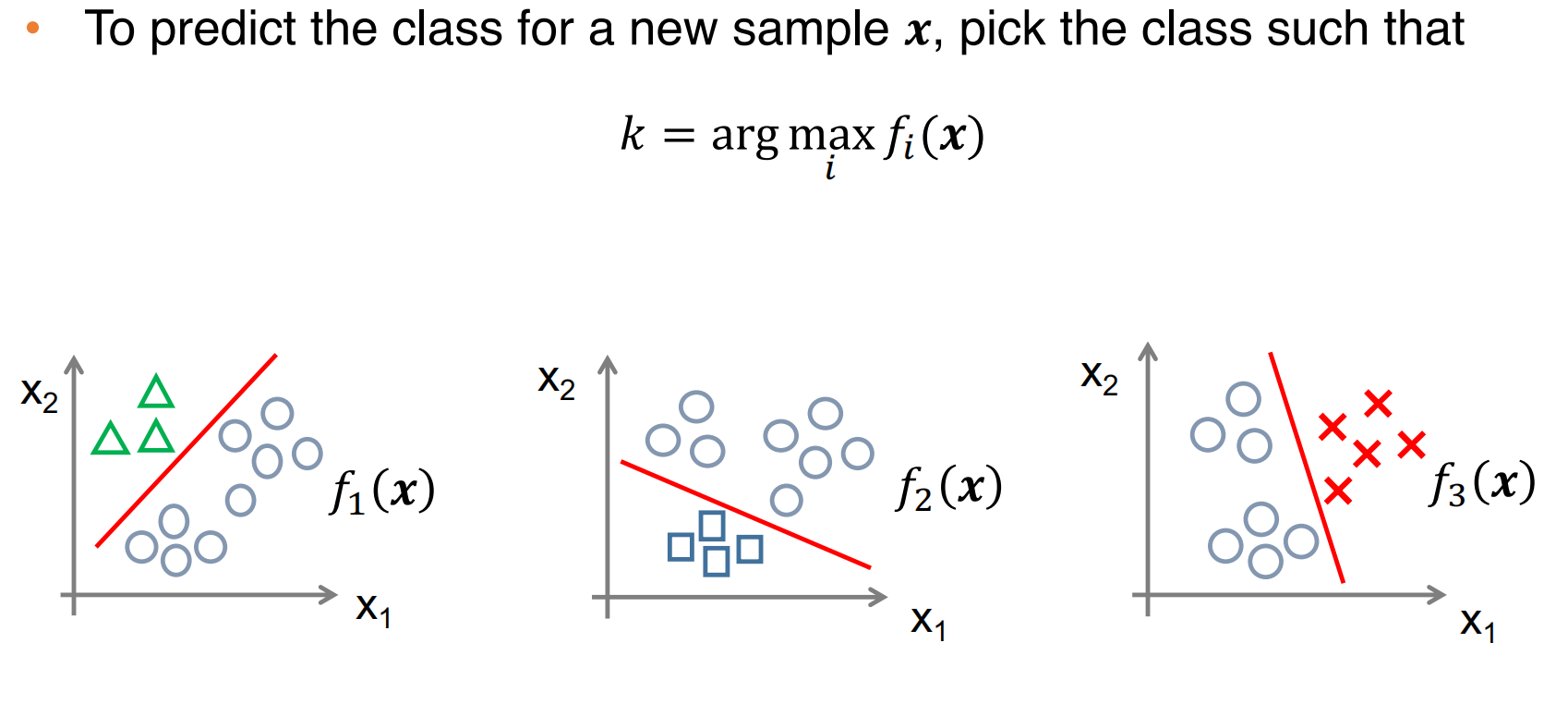
- softmax函数:数据x被分类到第i个类别的概率为:

对于二分类的softmax分类来说等同于参数为w1-w2的逻辑回归,原因如下:
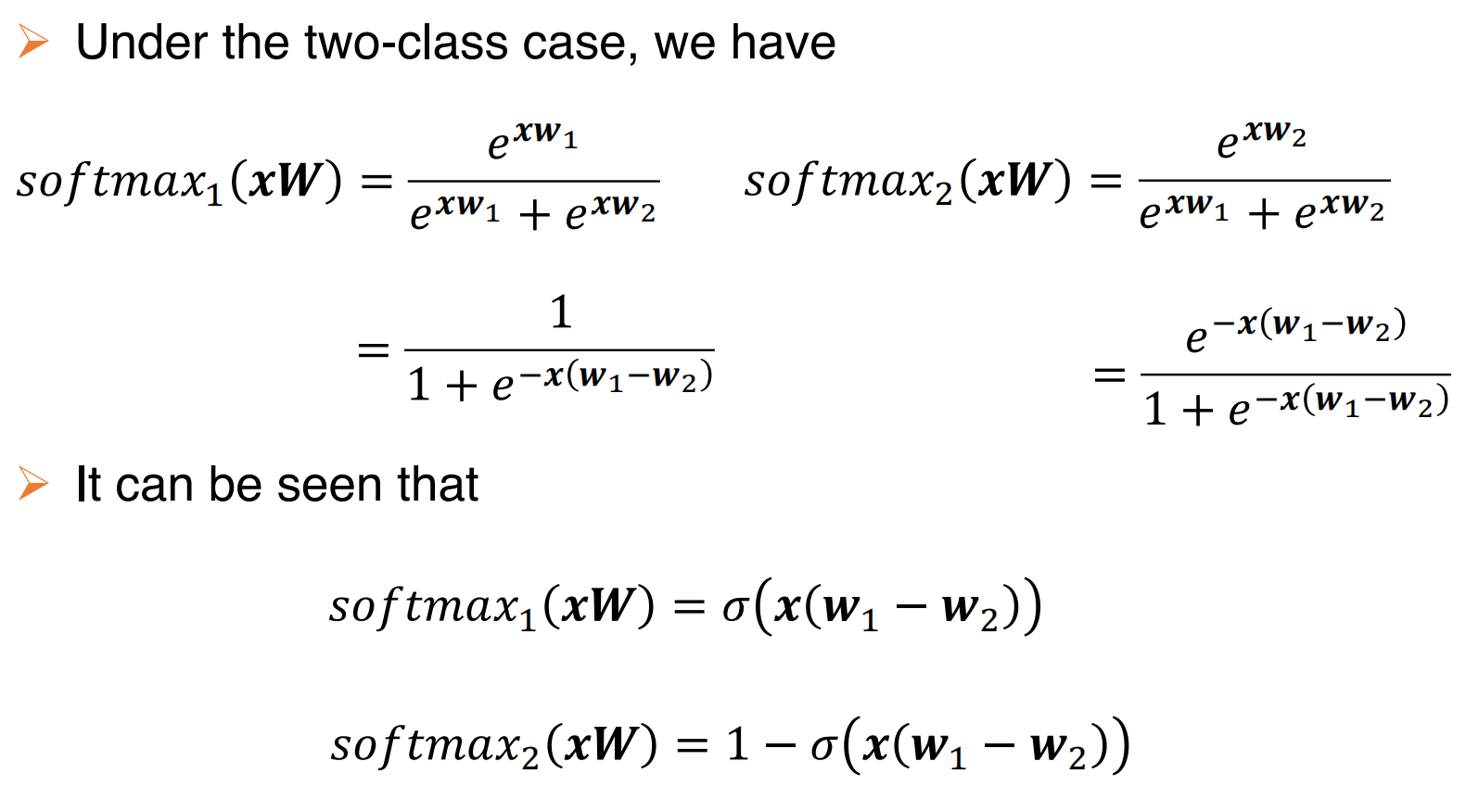
对于K分类来说,y标签是one-hot vector,损失函数如下:
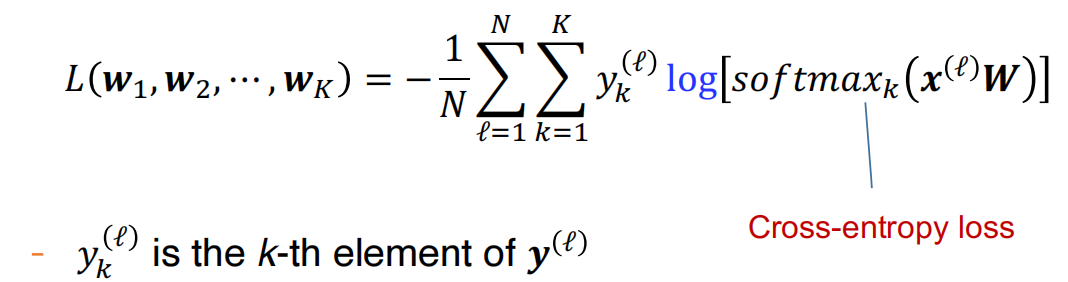
然后梯度下降:

从概率角度看回归和分类
Introduction
从概率的角度来看,给定\(x\)来预测输出\(y\),我们只需要对条件概率\(p(y|x)\)进行建模。
根据上面的这个条件概率,输出可以被预测为下面这两种形式:
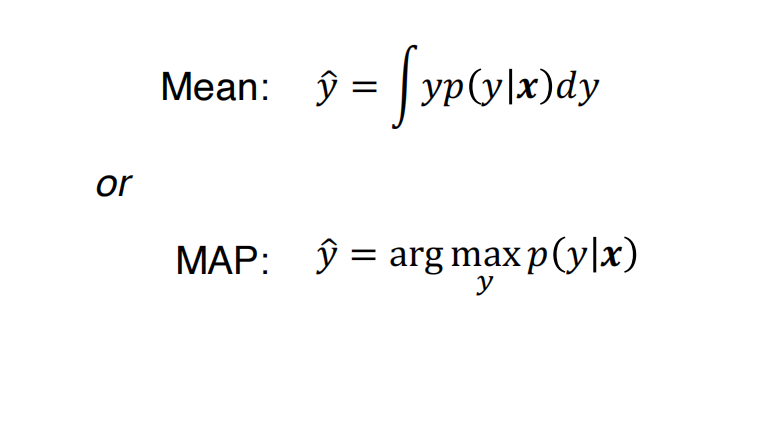
回归上的数学概率
单变量高斯分布:
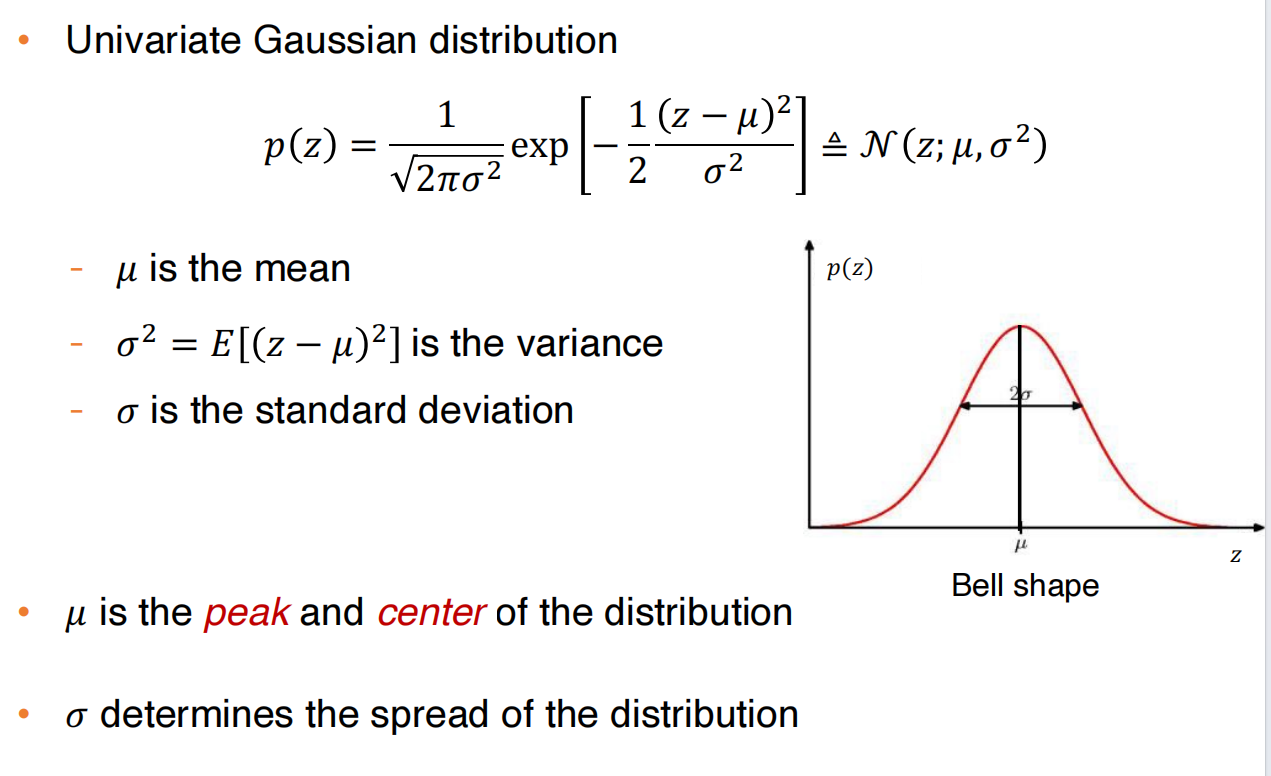
多变量高斯分布:
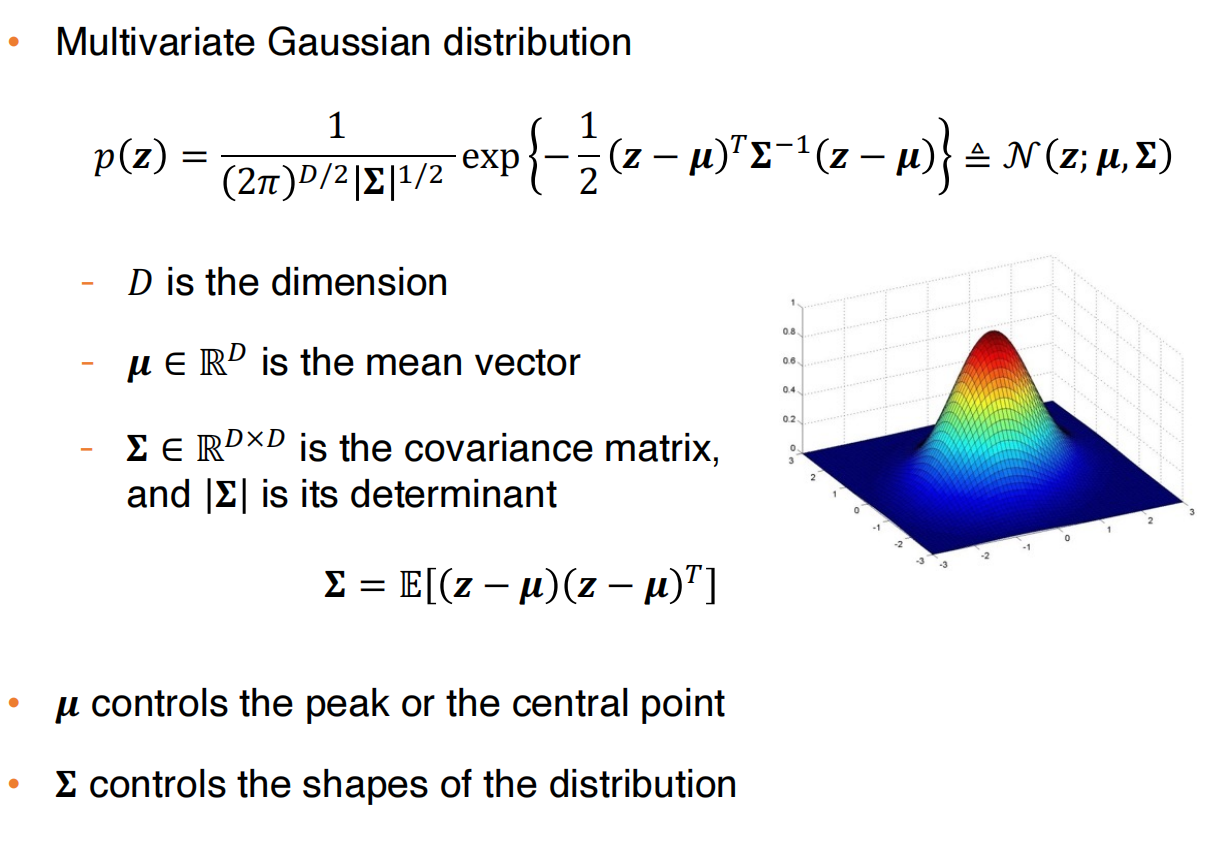
假设条件概率分布是正态分布,我们做一次预测,就是使用了条件概率分布的均值
模型训练的目的就是找到一个参数w,使得对数概率达到最大,如下所示,我们可以看到要最大似然函数就是要最小损失函数:

总结:
- 建模:假设条件分布为高斯分布
- 训练:训练模型就是最大化似然函数
分类上的数学概率
为了实现二分类,条件概率假设为伯努利分布:
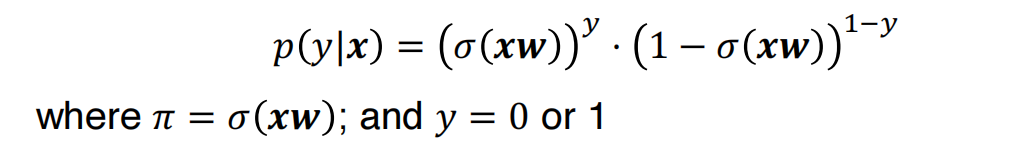
训练的目标就是最大化对数似然函数,可以发现最大化对数似然函数就是在最小化交叉熵:

总结:
- 建模:假设输出是伯努利条件分布
- 训练:训练就是要最大化对数似然函数
多分类问题
分类分布
\[ p(\mathbf{z} = \text{onehot}_k) = \pi_k \] - 其中\(\text{onehot}_i = [0,\cdots,0,1,0,\cdots,0]\)是一个向量,其中第\(i\)个元素是唯一的非零元素\(1\)。 - \(\sum_{k = 1}^{K} \pi_k = 1\)
该分布可以等效地写为
\[ p(\mathbf{z}) = \prod_{k = 1}^{K} \pi_k^{z_k} \] 其中\(\mathbf{z}\)是一个独热向量(one-hot vector)。
非线性模型 & 过拟合 & 正则化
非线性模型
怎样构建一个能够处理非线性建模的模型:
- 用基函数对线性模型进行非线性化
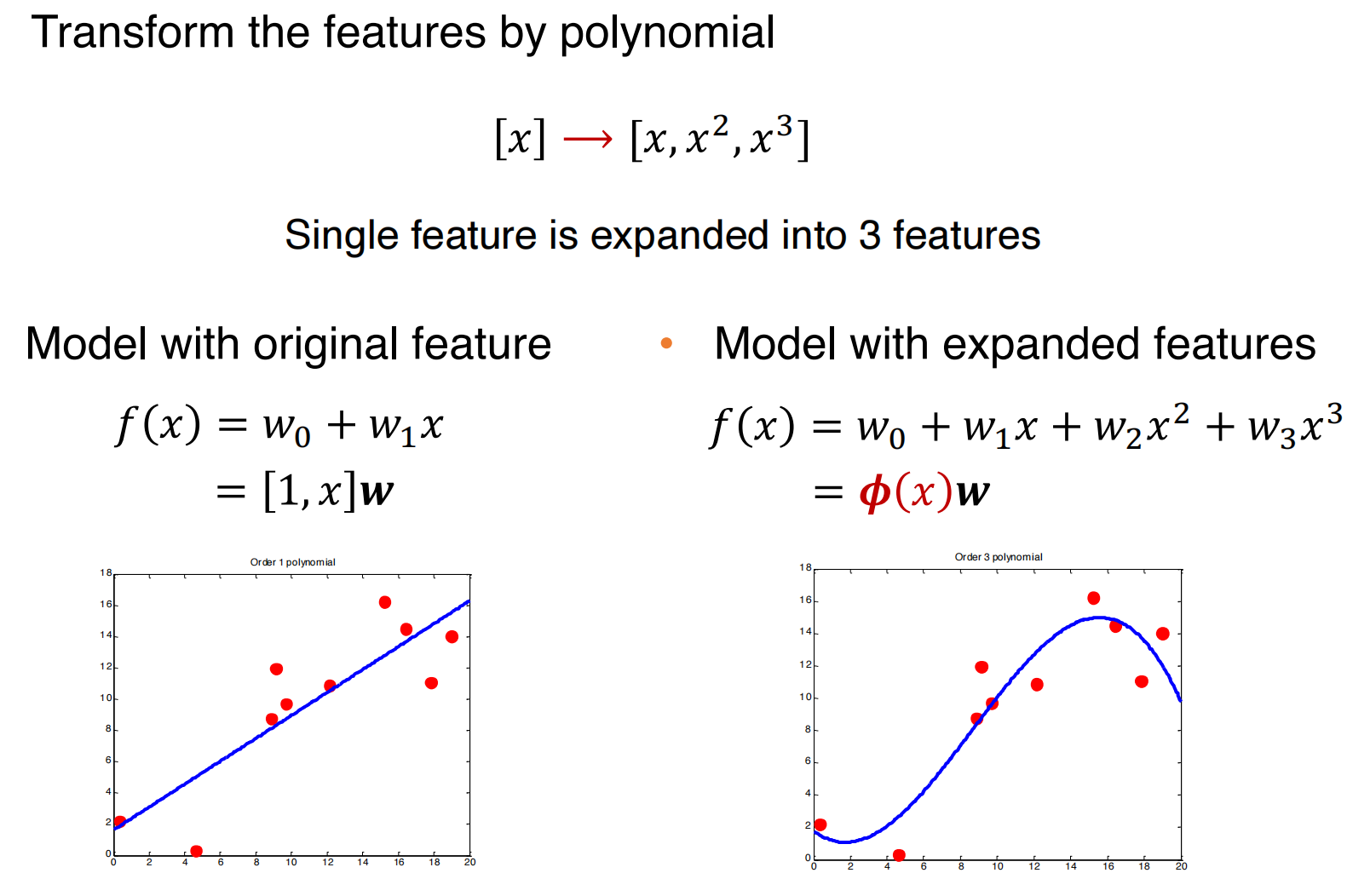
基函数模型:

基函数模型对x是非线性的,对于参数w来说仍然是线性的
过拟合
模型在“看不见”的数据上表现良好的能力叫做泛化能力
通常来说,模型的复杂度取决于参数的数量,参数越多,模型越复杂。
赤池信息标准:

贝叶斯信息标准:

由于似然函数,上述标准只能用于概率模型
为了让模型表现良好,我们应该平衡模型的复杂性和表示能力
如何验证误差随着模型的复杂度增加而减少,它表明模型欠拟合,否则,它表明模型过拟合
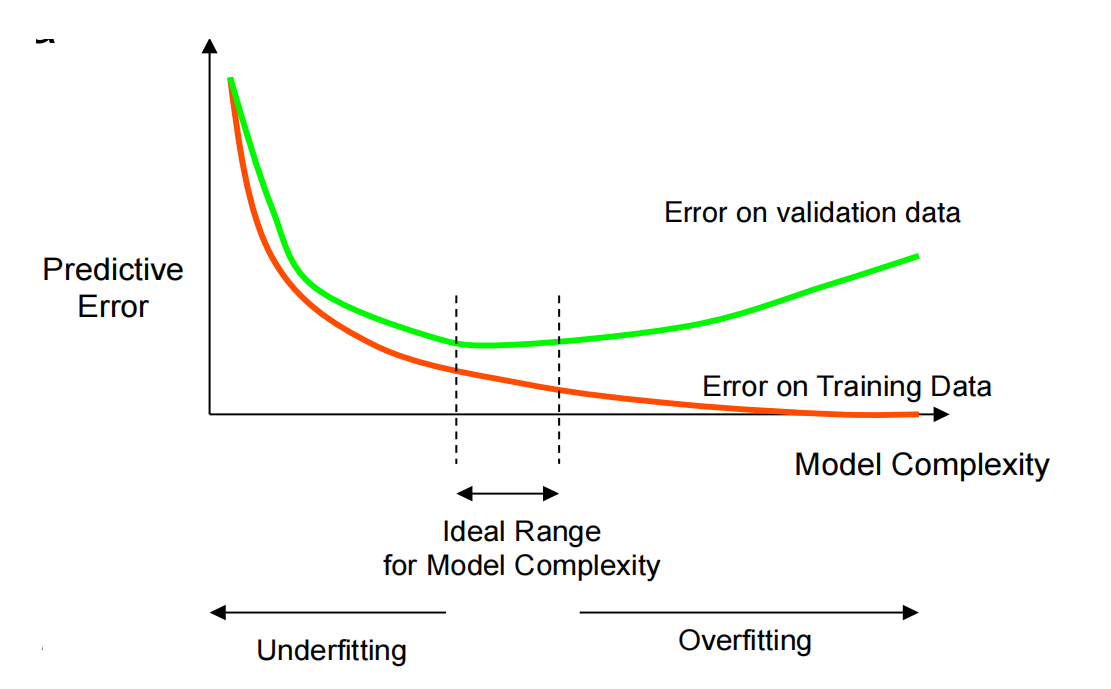
如果训练数据给太多给验证集,则没有足够的数据样本用于训练
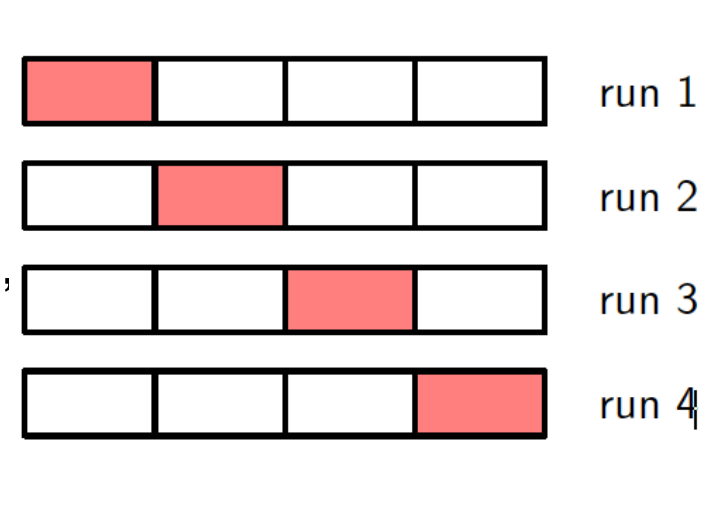
K-fold cross-validation(K折交叉验证):
- 把训练集分成K个子集
- 在K-1个子集上进行训练,在一个子集上进行验证
- 重复K次,每一次都使用了一个不同的子集用以验证
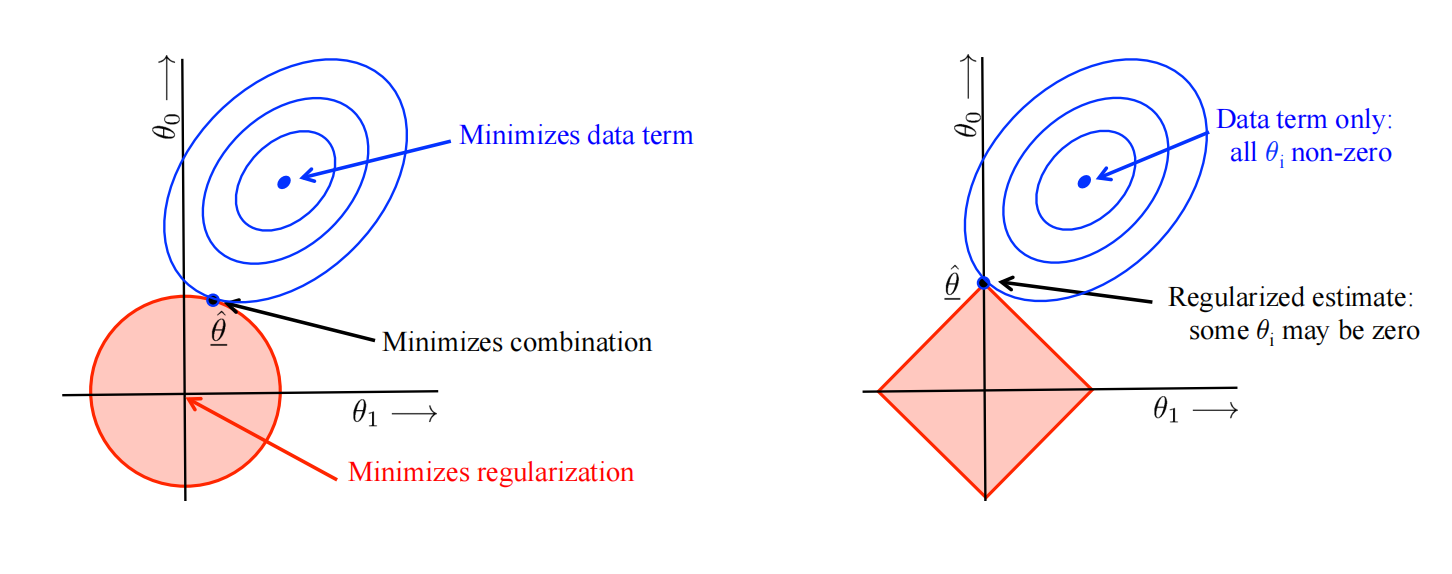
\(L_2\)正则:

- 容易把模型的参数缩小到0
- \(\lambda\)的值越大,对较小的w的偏爱就越强
\(L_1\)正则:

L1正则同样更喜欢值更小的模型参数,但是L1经常导致w的稀疏解,即参数中很多值为0
支持向量机
线性分类器的决策边界
在线性分类器中,决策边界总是一个超平面,它的目标就是找到一个超平面能够分隔开所有的样本
比如逻辑回归,通过最小化交叉熵来找到决策边界超平面:

并且具有以下性质:
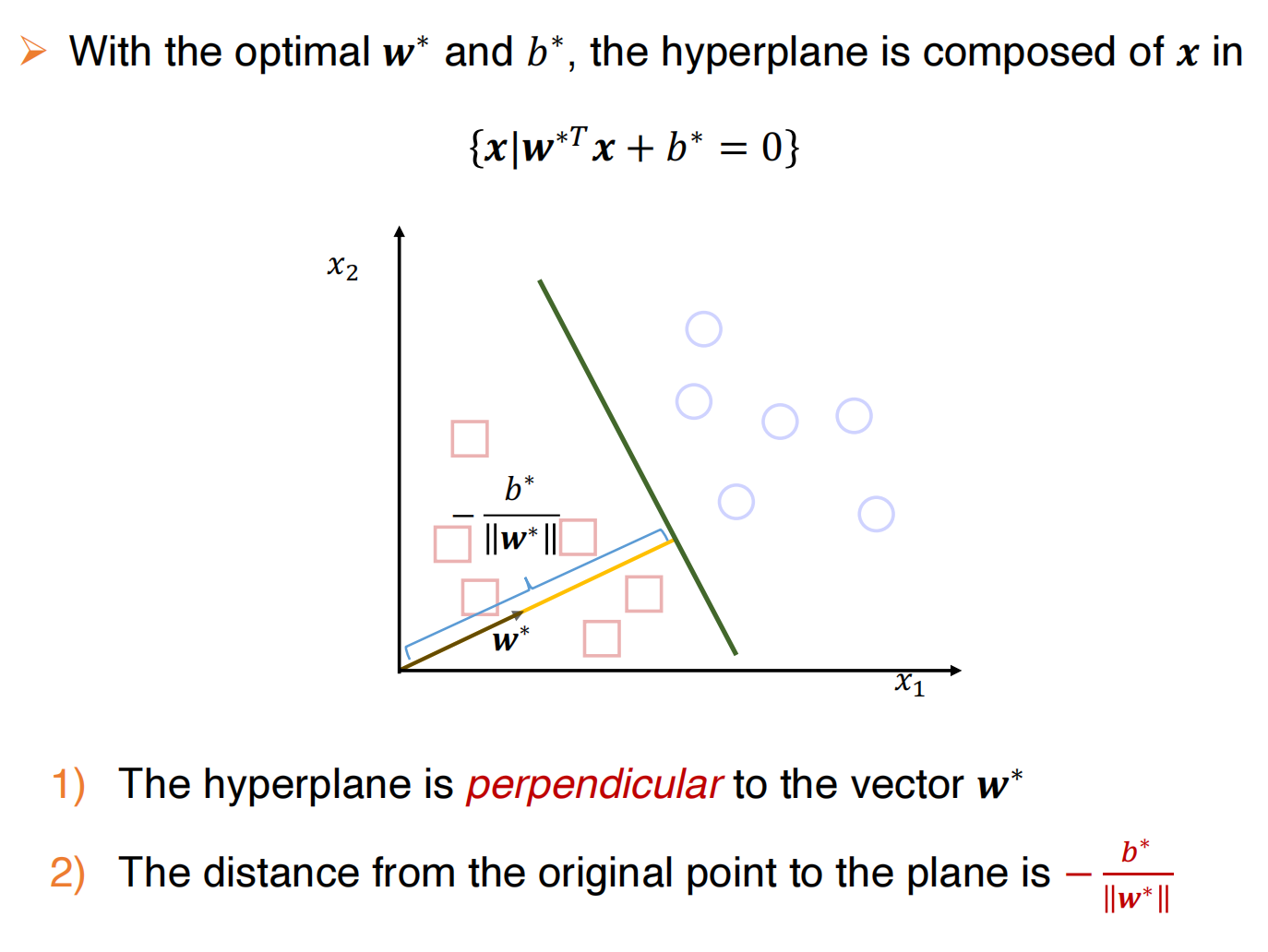
对于不同的损失函数,我们可以得到不同的超平面,比如说下图:
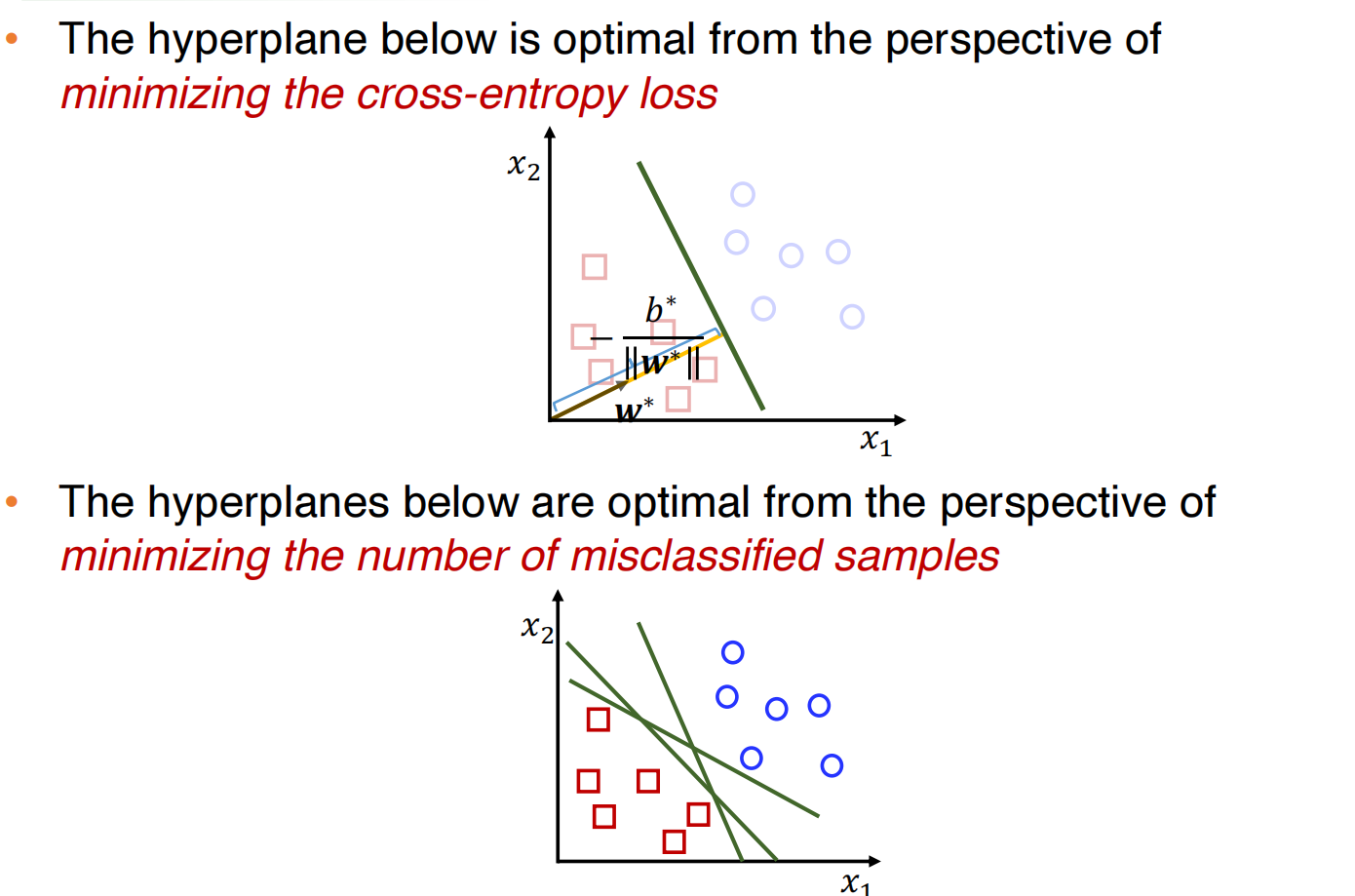
但是这些超平面都是在训练集上进行评估的,但是我们需要的是在测试集上较好的性能,那怎么评估一个超平面的好坏呢,一个简单的直觉就是,最大化边界。
线性最大化边界分类器
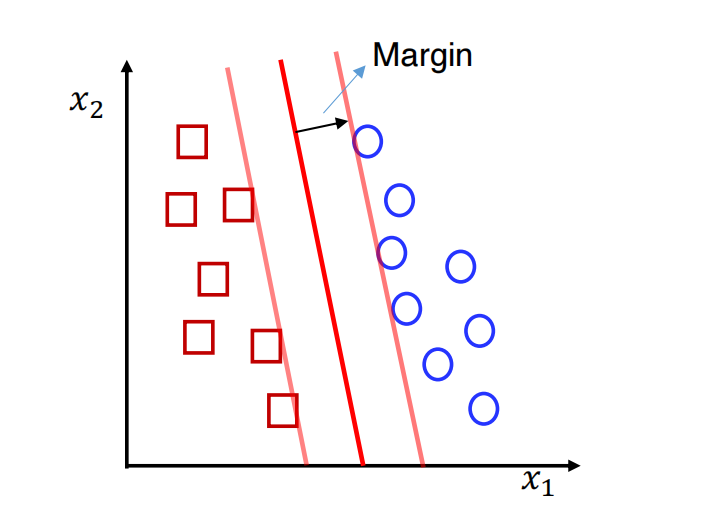
如上图所示,边界越大,那么在没有看见的数据集(测试集)上它能够正确分类的概率就越大。
怎么表示边界?

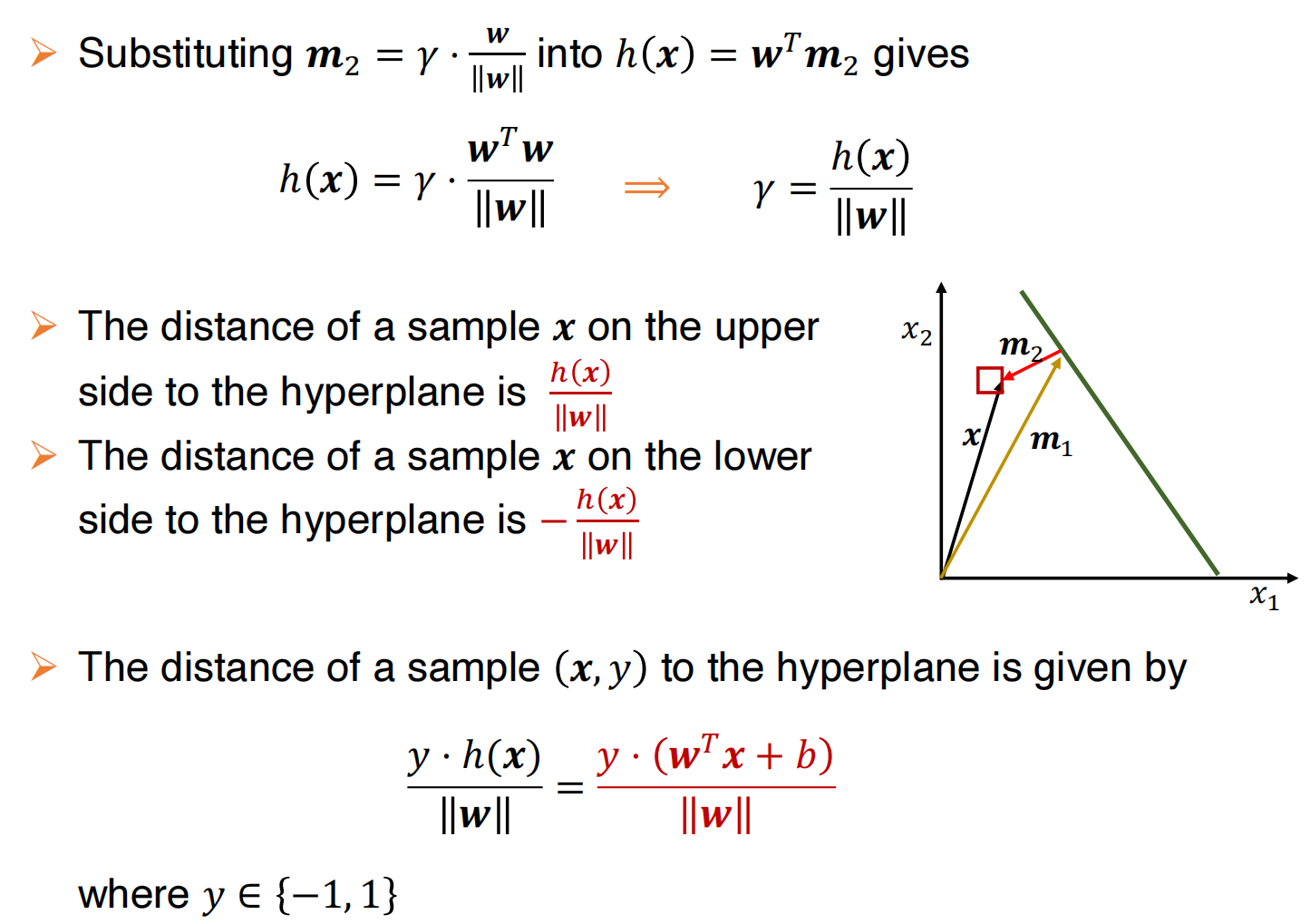
边界就是所有点与超平面的最小距离,因此最大边界分类器的目标就是找到最优的w和b,使得边界最大,即:
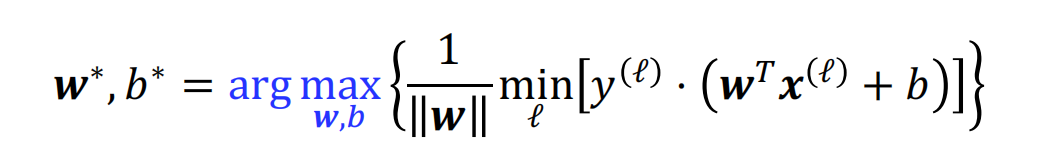
转换后的目标函数
basic idea:优化一个与原始问题共享最优值的目标函数

如此的话我们可以得到一个具有相同最优值得目标函数,这是一个带约束得目标函数:

因为至少有一个等于符号成立,目标函数可以化简为:

进一步转换:

因此最大边界超平面就能通过以下优化函数找到:
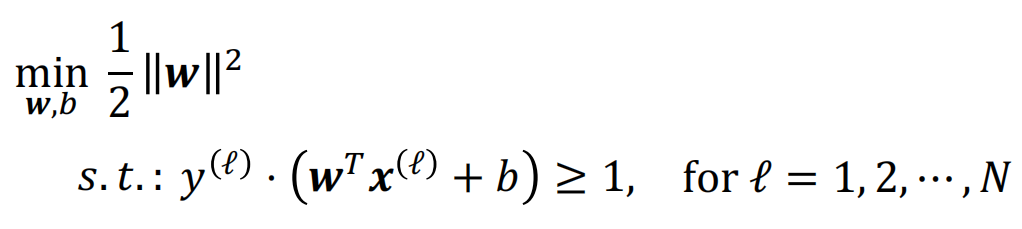
这是一个二次型优化问题,可以通过数值方法求解:
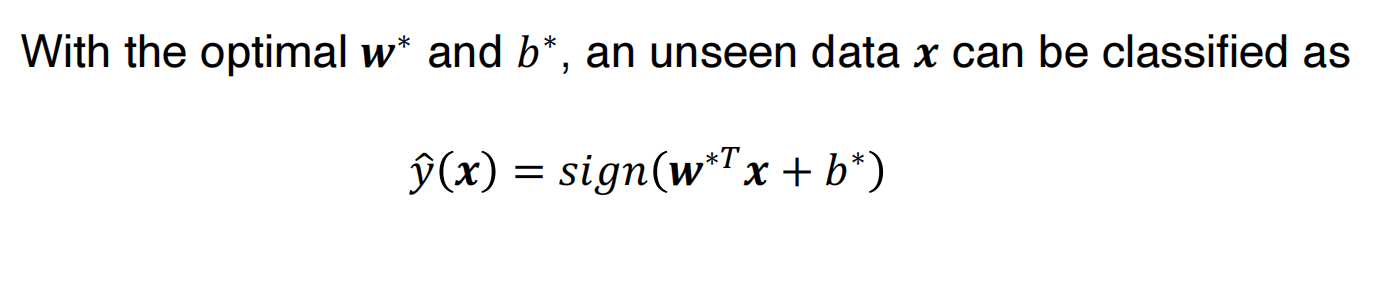
等效的对偶公式
每一个凸优化问题都有相应的对偶公式
原始优化问题的拉格朗日函数:

求解该拉格朗日函数:

因此,对偶的优化变成:

w,b,a之间的关系:

至此我们得到了原始分类器的对偶版本:

如何理解对偶最大边界分类器:

an的稀疏性
测试的复杂度貌似更高

支持向量:在边界上的那些样本被称作
不等式的约束条件使用拉格朗日法需要满足KKT条件,即是下图红色部分,可以推出大部分an都是0

因此测试的函数可以化简为: