算法设计与分析课程笔记
分治策略
分治算法基本思想
将大规模的原问题分割成k个更小规模的子问题,如此递归地进行下去,知道子问题规模足够小,能够很容易求出解为止。
子问题和原问题具有相同的性质
子问题求解尽可能独立
各个子问题的规模尽可能均衡
三个阶段:
- Divide
- Conquer
- Combine
一般选择性问题
问题:选择出乱序数组中第k小的数
算法:
- 暴力:时间复杂度:
- \(O(kn)\)
- 排序:
- \(O(n\log n)\)
- 分治:

算法的效率依赖于子问题的规模,所以寻找m*很重要。采用如下的划分
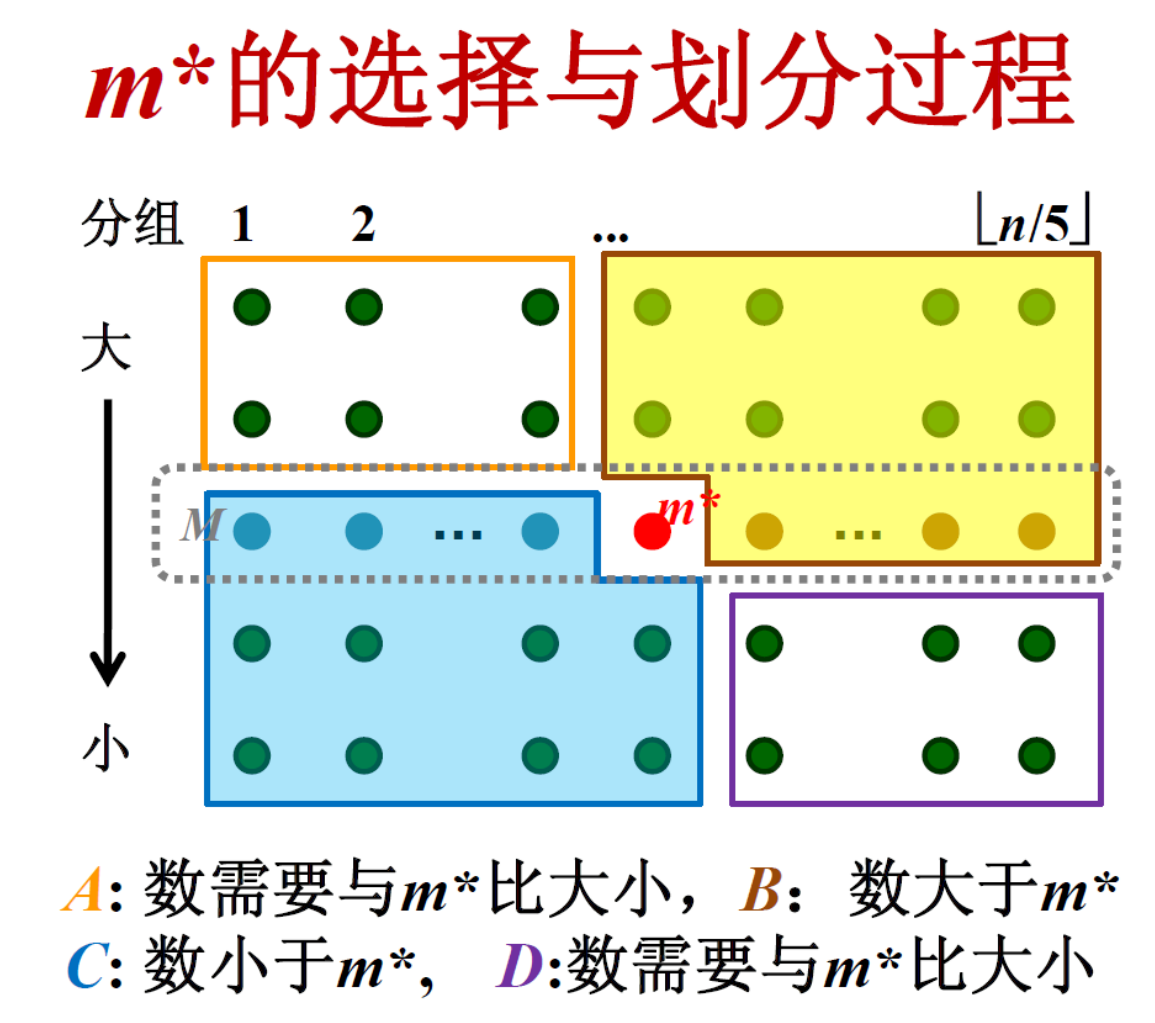
可以得到子问题规模
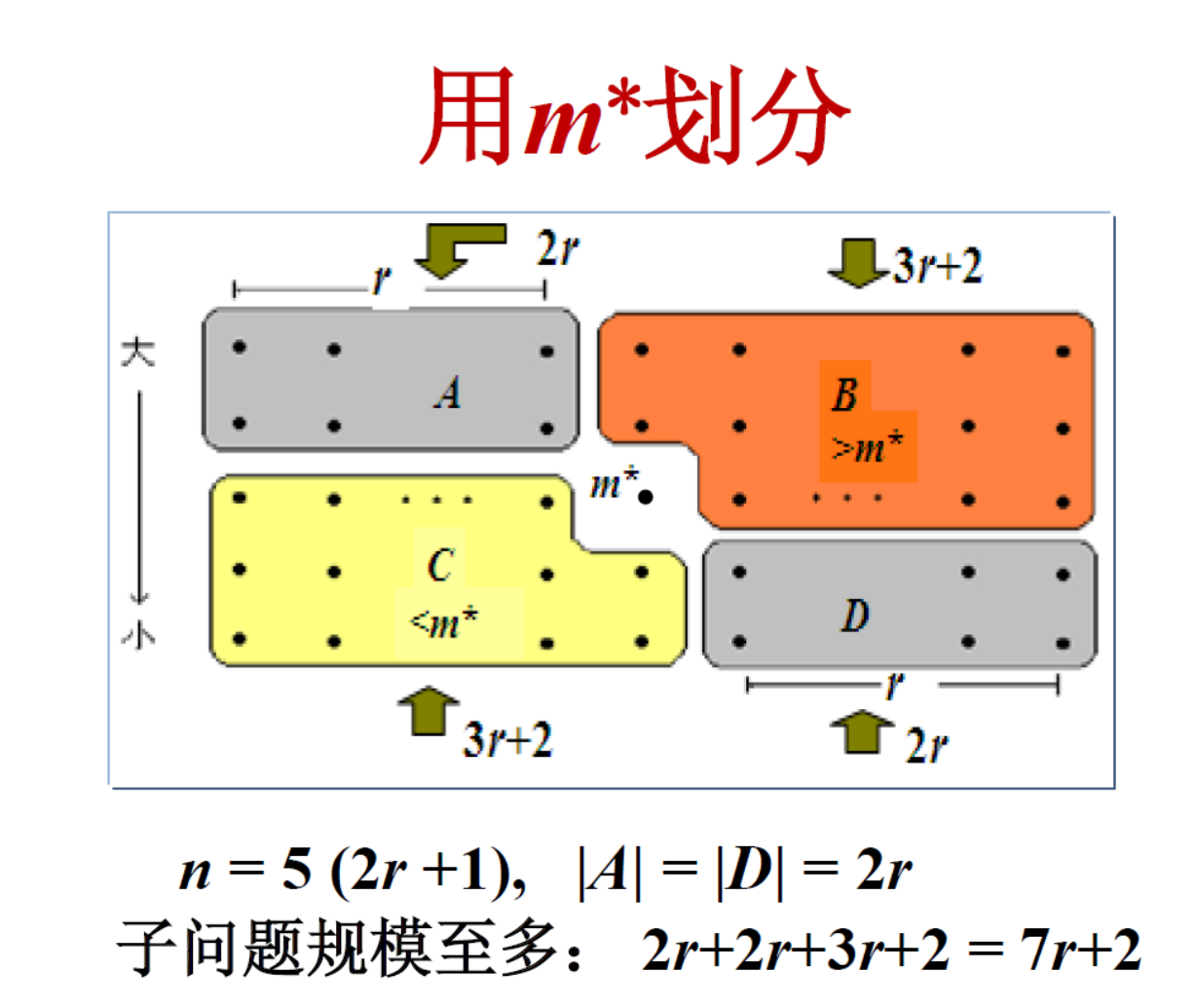
时间复杂度

采用递归树的方式求解时间复杂度:
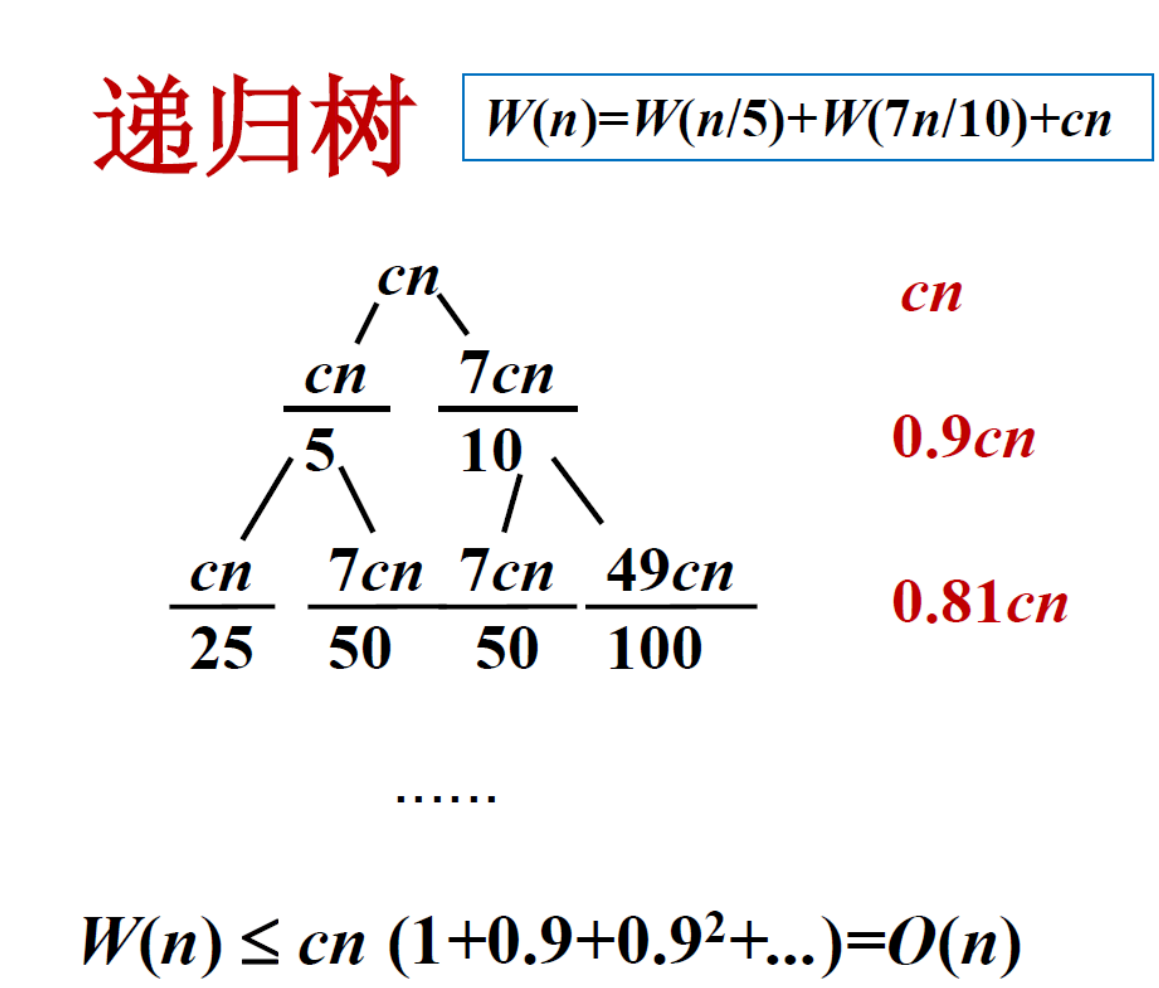
平面点集的凸包
问题:给定大量的离散的点,求解一个最小的凸多边形,要求所有点都在边上或者多边形内部
分治:
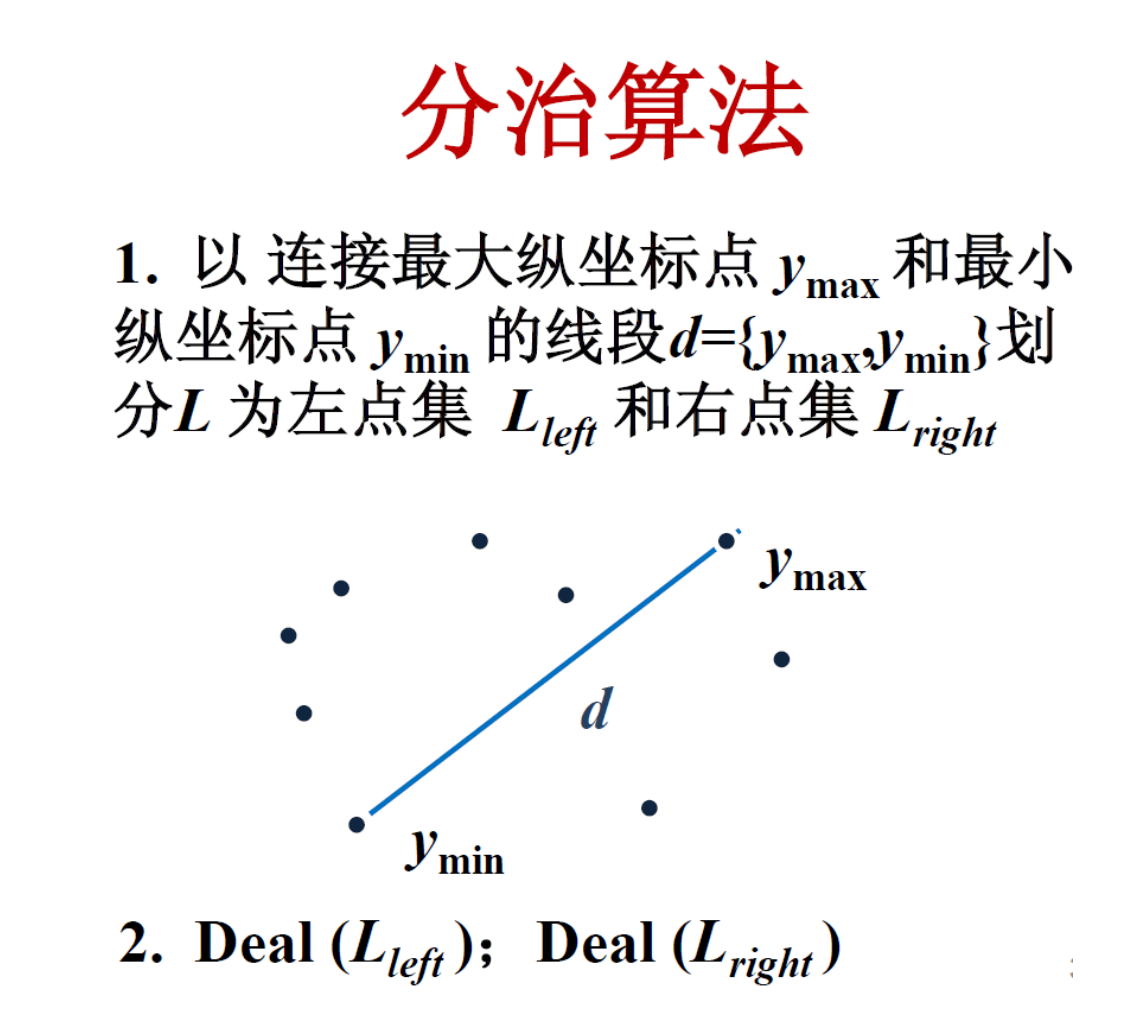
子问题:
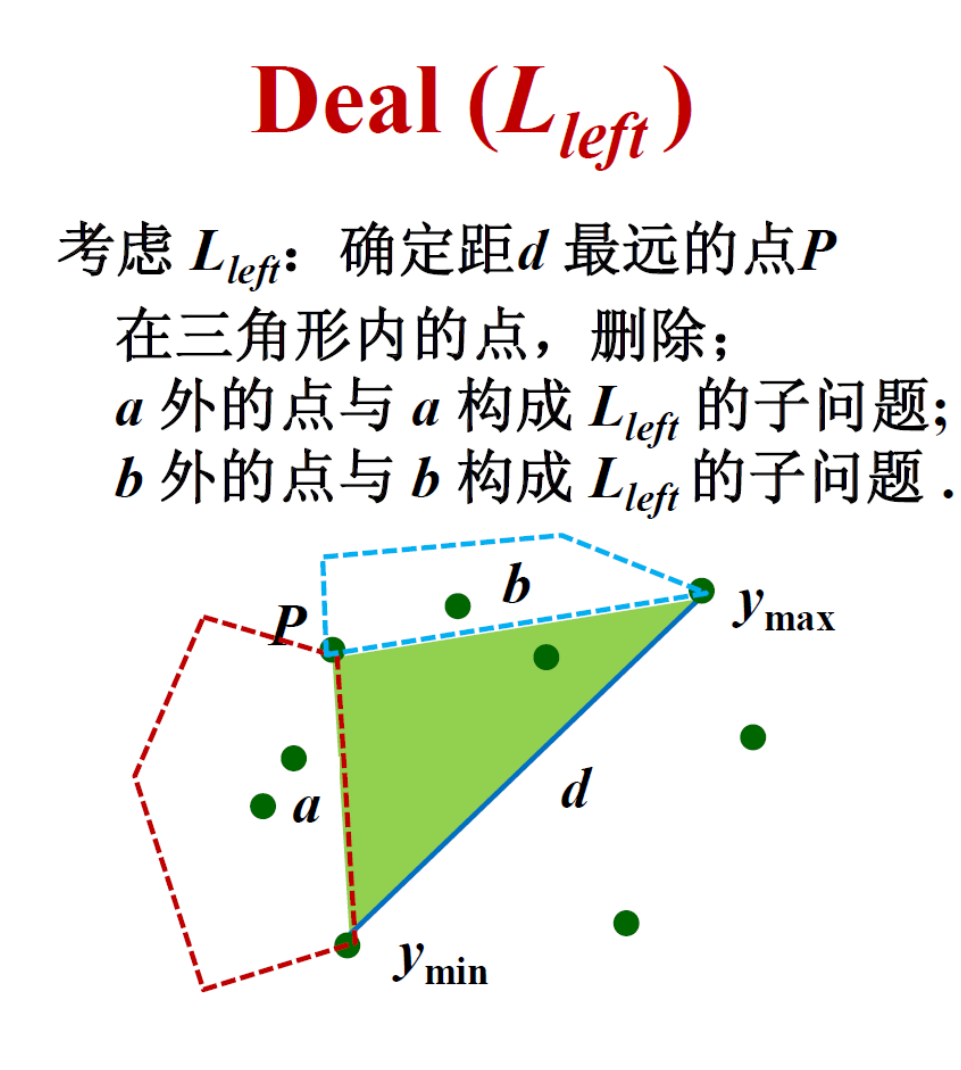
动态规划
二进制数排列

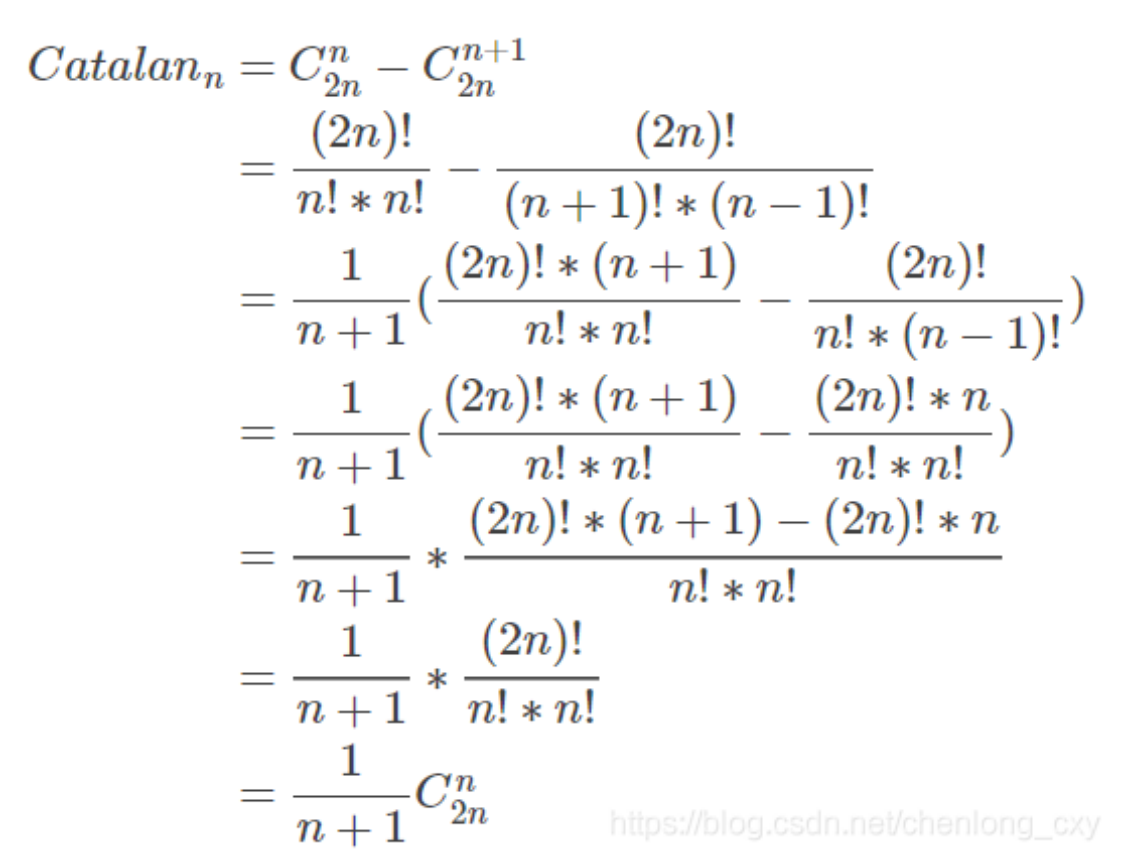
矩阵链相乘
问题

例子

动态规划
子问题的划分如下

得到递推方程

时间复杂度分析
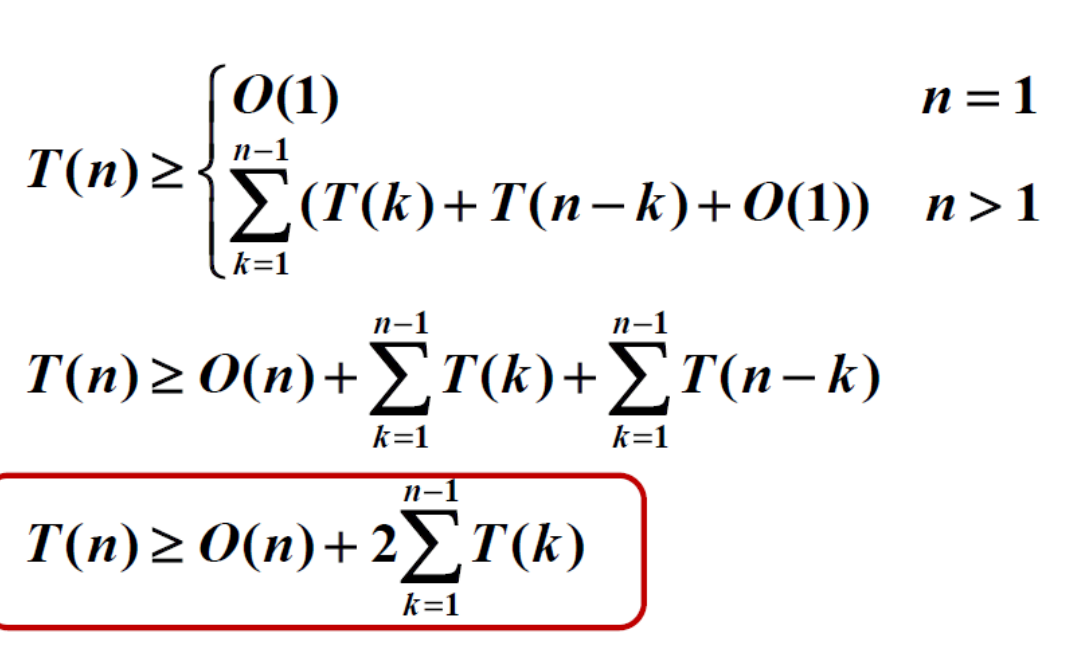
时间复杂度仍然较高,因为有大量子问题重复

迭代计算

黑白图像存储

可以用以下方法优化存储

这样就得到一个问题,如何确定最优分段

可以得到如下递推方程

最大子段和
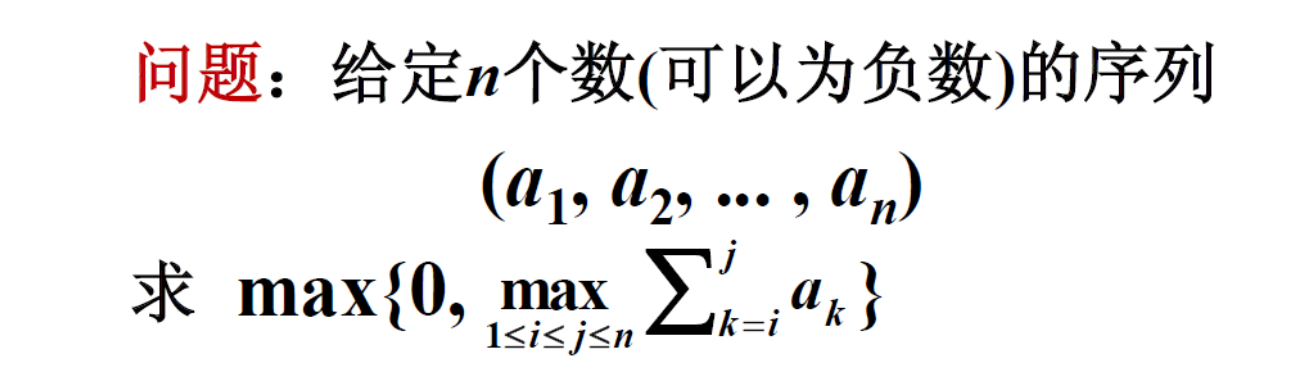
可以想到以下三种方法

算法2(分治):

算法2的时间复杂度:
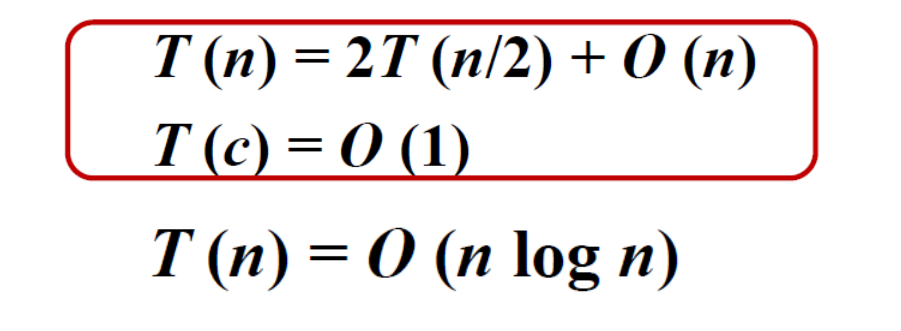
算法3(动态规划):
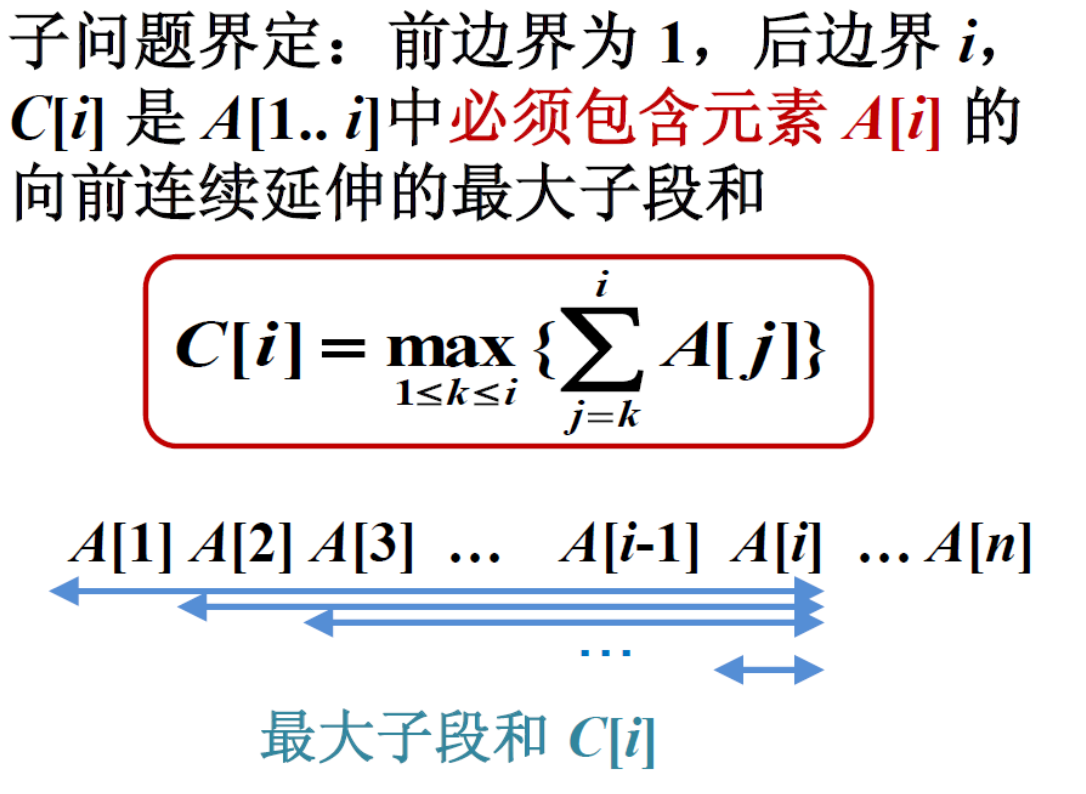
得到递推函数:

序列的编辑距离

i,j是两个序列的边界,若\(s_1[i]\ !=\ s_2[j]\)则需要选择删除,插入或替换操作,从而带来编辑距离的增加
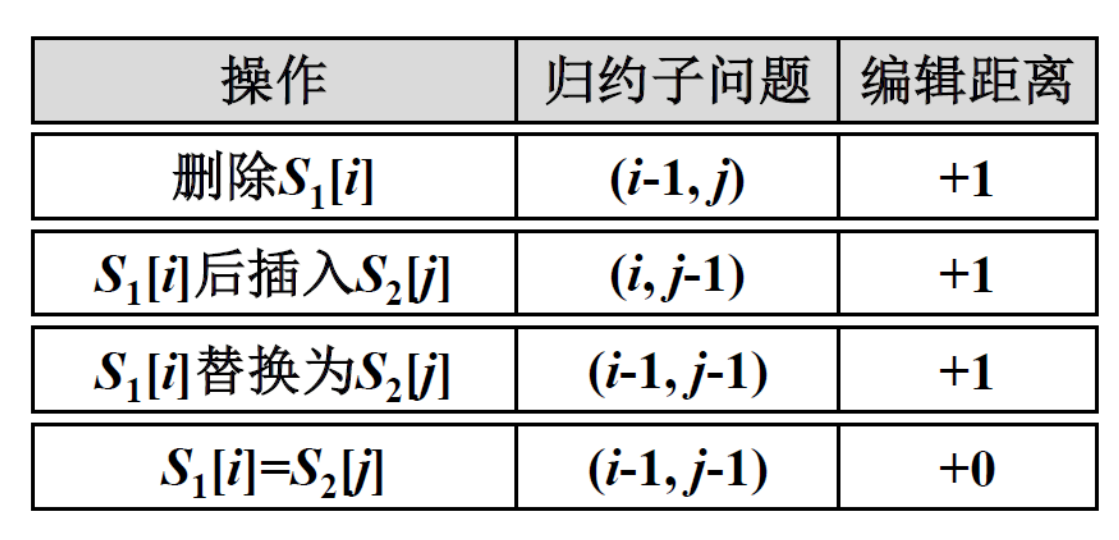
因此得到以下递推方程

贪心
多机调度问题

可以得到以下定理,得到近似比为(2-1/m):

证明过程如下:

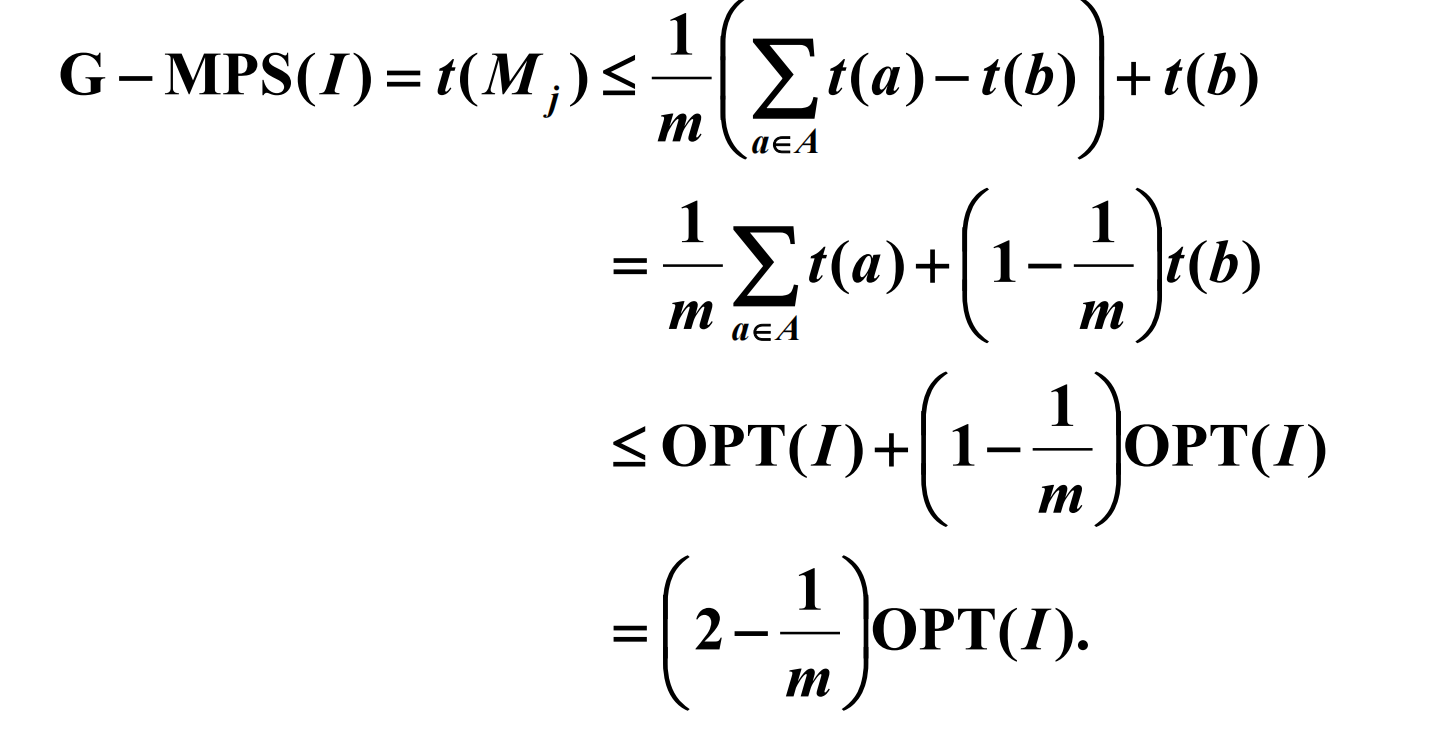
改进的贪心法,先排序

可以得到近似比如下,注意括号前面的1/m是错误的

近似比的证明:

最优前缀码

可以退出两个引理为:
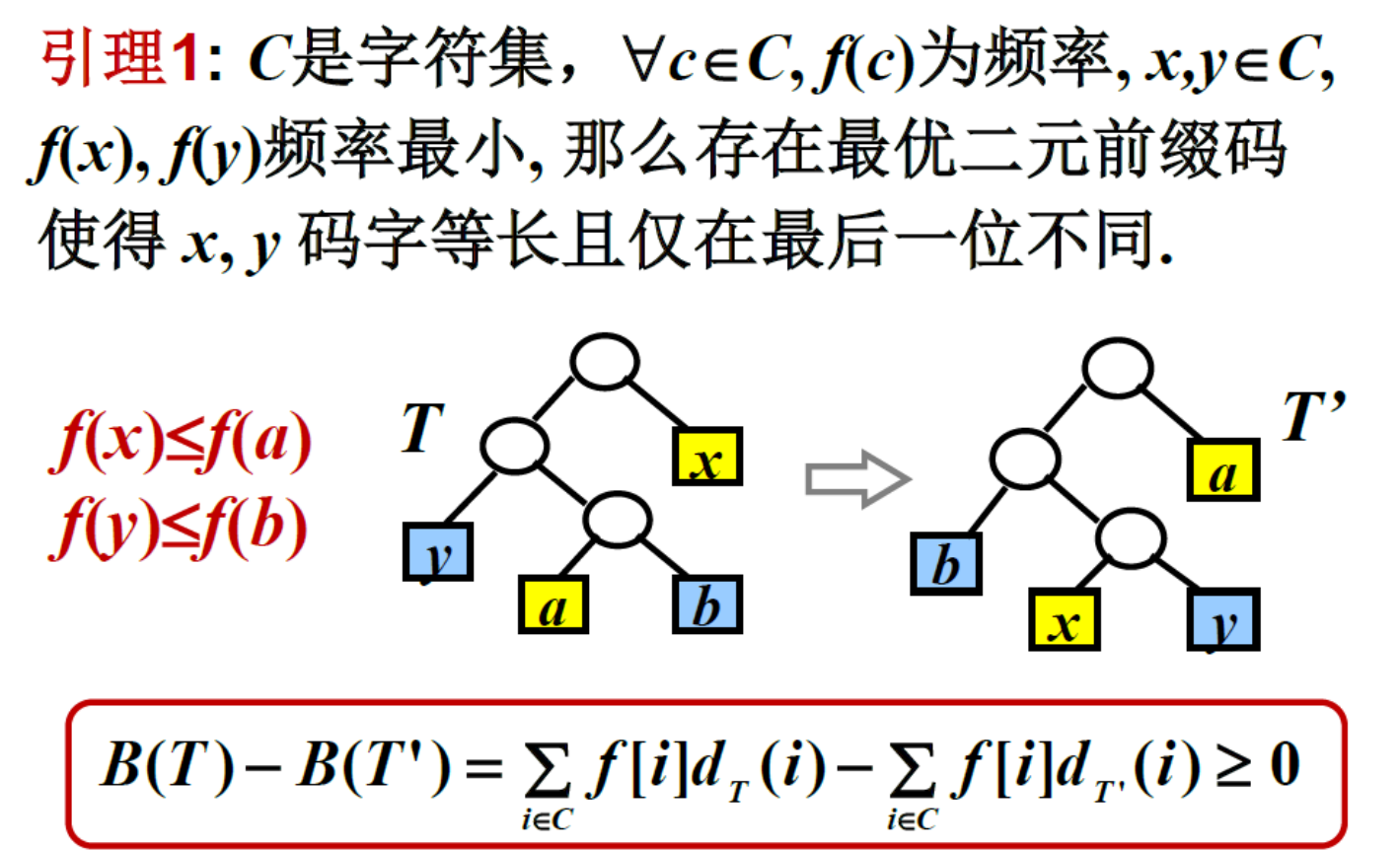
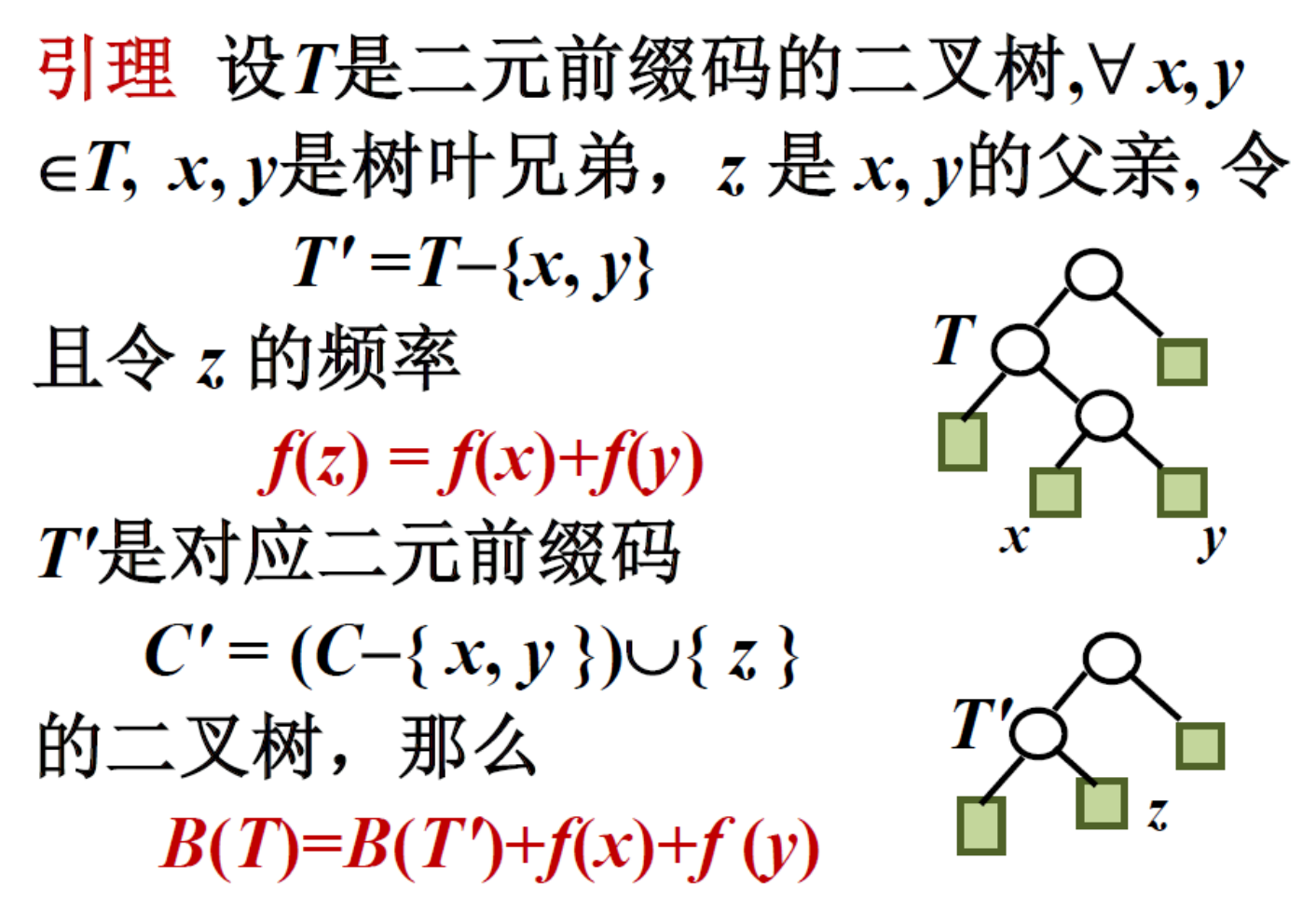
使用刚刚的引理,证明Huffman算法的解为最优解:

最小生成树
prim

kruskal

单源点最短路径
dijkstra,只适用于没有负权边的情况

如果源点存在可达负环,则最短路径难以定义,因为可在环中一直循环,权重可以达到负无穷。
Bellman-Ford算法:
- 如果存在负权边,如何找到单源点最短路径:每一轮都对所有边进行松弛,持续迭代|V|-1轮
- 如果存在负权边,如何发现是否有负环存在:若第V轮仍然松弛成功,存在单源点可到的负环
Bellman-FordSPFA:
是对Bellman-Ford算法的优化。Bellman-Ford算法在每次更新时,遍历了所有的边,而也如前面看到的,每次遍历未必会真的更新最短距离。SPFA算法就是对该步骤的优化。每次只有当前的起点到源点的距离变小了,该点连通的其他点才会变小。只要一个结点的边变小了,我们就把他放进队列(其他的也行)中,只要队列中还有值,我们就继续更新,更新到的点也加入队列,如此往复,直到标记全部的点。
回溯
货郎问题

可以得到这样的界和代价函数:

连续邮资问题

算法设计:

确定r_i:

网络流算法
最大流问题

定义最小割集:
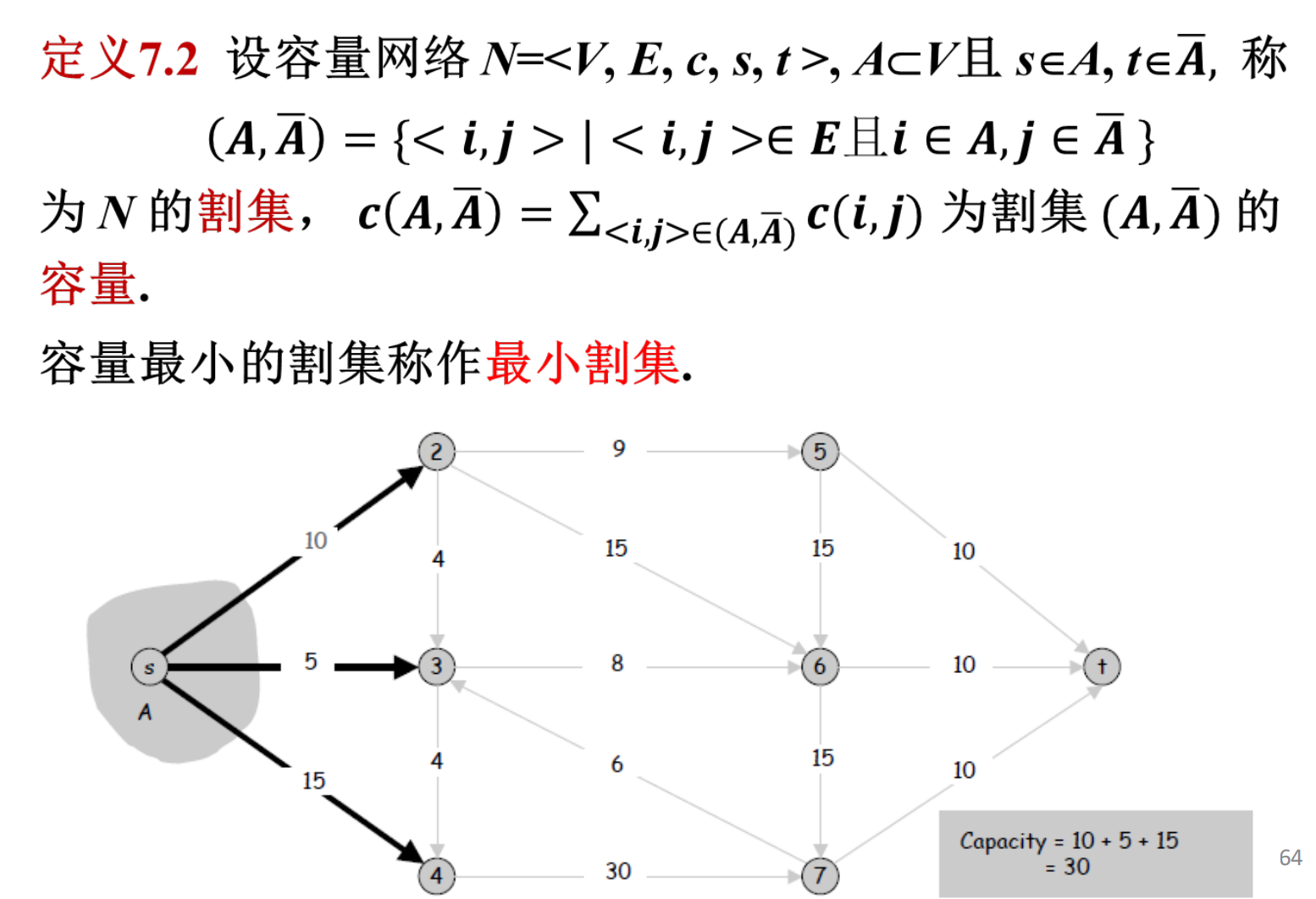
可以得到如下引理:

因此最大流问题转换为了找最小割集
增广链概念:

