中山大学人工智能课程复习笔记
绪论
人工智能三大学派
- 符号主义,又称为逻辑主义
- 连接主义,又称为仿生学派
- 通过模拟人类的神经元来模拟人类的智力活动
- 代表工作:人工神经网络
- 缺点:缺乏可解释性
- 行为主义,又称为控制论学派
- 认为智能行为的基础是“感知-动作”的反应机制
- 代表工作:强化学习,演化算法,Brooks六足行走机器人
知识的表示与推理
一阶逻辑(谓词逻辑):文法和语义
项:
- 每个变量都是一个项
- 如果\(t_1,...,t_n\)是项,\(f\)是一个n维函数,那么\(f(t_1,..,t_n)\)是项
公式:
- 如果\(t_1,...,t_n\)是项,\(P\)是一个n维谓词,那么\(P(t_1,..,t_n)\)是原子公式
- 如果\(t_1,t_2\)是项,那么\((t_1=t_2)\)是原子公式
- 如果\(\alpha,\beta\)是公式,\(v\)是变量,那么\(\neg\alpha,\alpha\wedge\beta,\alpha\vee\beta,\exist v.\alpha,\forall v.\alpha\)都是公式
变量辖域:一个变量\(x\)在一个公式\(A\)中是这样的形式出现的:\(\exist xB,\forall xB\),其中B是A的子公式,则x是约束出现,否则都是自由出现
句子:一个没有自由变量的公式
置换:\(\alpha[v/t]\)意味着\(\alpha\)中所有自由出现的变量v被替换成t
解释:M=<D,I>
- D是论域,非空集合
- I是一个来自于谓词和函数集合的映射

指称:一个变量赋值\(\mu\)表示一个从变量到论域的映射
\(M,\mu\vDash\alpha\):读作\(M,\mu\)满足\(\alpha\)
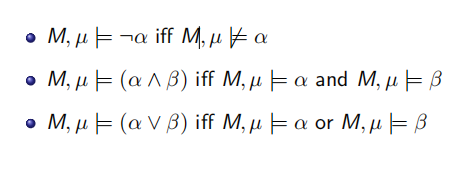
如果\(\alpha\)是一个句子,则\(M,\mu\vDash\alpha\)与\(\mu\)无关,所以可以直接写成\(M\vDash\alpha\)
可满足性:
- 如果S是一个句子的集合,M满足S,则称M是S的一个模型,如果存在M可以满足S,则称S是可满足的
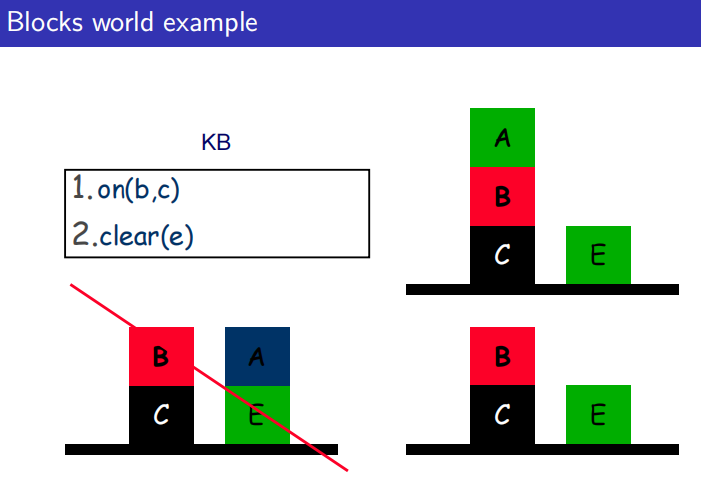
逻辑蕴含:S |= α 当且仅当对任意一个 M, 都有如果 M |= S 则 M |= α
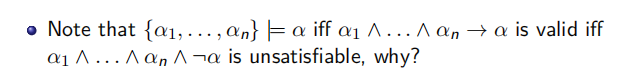

基于归结的推理过程
把S当作KB知识库,如何证明知识库可以满足\(\alpha\)就需要用到归结推理。
文字:原子公式和它的非
子句:子句是文字的析取,如果一个公式是合取,需要写成析取的集合
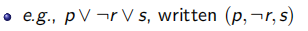
消除掉子句中那些冲突的文字的这个过程叫做推导
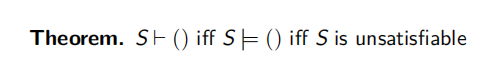
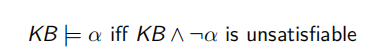
所以确认KB是否满足\(\alpha\)的过程为:
- 把KB和\(\neg\alpha\)写成子句形式得到S
- 确认S是否可以推导\(\alpha\)
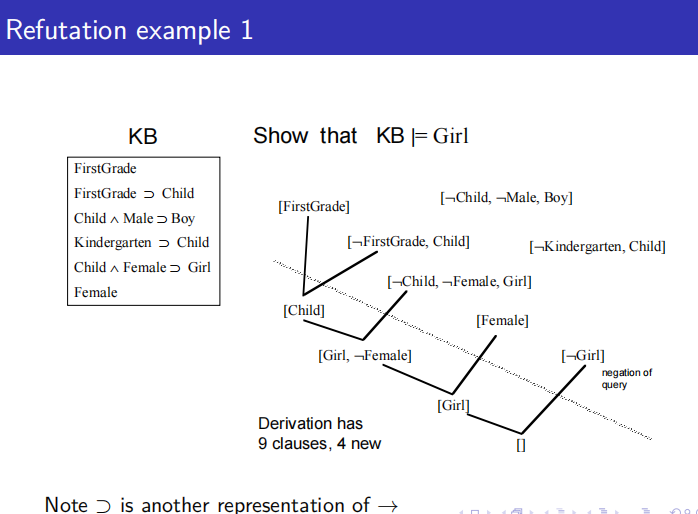
对于一阶逻辑的情况我们需要重新考虑以上两个步骤
转为子句的过程:
- 消除蕴含符号
- 否定内移,移动到谓词前,量词记得变换
- 变量标准化,不同变量使用不同符号
- 消除存在量词:使用一个新的常量代替此前的存在量词下的变量,若存在量词前有全称量词,则使用一个由全称量词变量组成的函数去代替存在量词下的变量
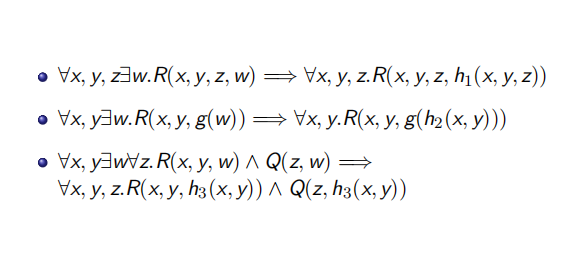
- 转换为前束范式,
- 转为合取范式
- 子句化
合一:找到冲突文字即使文字中有变量,然后将两个子句合为一个子句。
合一的一个重要组成是置换,注意不是所有公式都可以合一,只有变量有置换
合一项:使得两个公式语法相等的一个置换
最一般合一项(MGU):对于其他合一项,一定可以写成最大合一项合另一个合一项的复合
计算MGU的过程:

这样得到的合一项一定是最一般合一项,同时也得到了合一后的子句,从而推出一个新的子句。
注意每一次循环都要对S进行置换
这样我们就有了归结的全部过程:

对于存在性的查询,我们还可以给出具体的答案,过程如下:

盲目搜索
搜索问题的形式化定义
- 搜索的状态空间
- 使状态发生改变的动作集合
- 初始状态
- 目标状态
搜索算法
输入:
- 初始状态
- 后继函数S(x,a):返回在状态x通过动作a可以到达新状态的集合
- 目标检测函数
- 单步的代价函数C(x,a,y):返回从状态x通过动作a到状态y的代价
输出:
- 从初始状态到目标状态的一个状态系列
树搜索
- 边界是我们还没有探索但是想探索的状态
搜索的关键性质
完备性:如果有一个解,搜索能否一定找到解
最优性:搜索能否总是找到最小代价的解
时间复杂性:所生成或扩展过的节点的最大数量
空间复杂性:必须保存在内存中的节点的最大数量
宽度优先搜索
总是选择边界上的第一个节点进行扩展
令b为任何状态的后继状态的最大数量,令d为找到最优解的动作数量

深度优先算法
将当前状态的后继放在边界的前面,因此总是扩展最深的节点
完备性:
- 无限状态空间:无
- 有限状态空间,但是有无穷条路径:无
- 有限状态空间且没有重复路径:有
最优性:无
令m为状态空间中的最长路径长度
时间复杂度:\(O(b^m)\),很差如果m远大于d
空间复杂度\(O(bm)\),线性空间
一致代价搜索
边界上的路径按代价的增序排列,始终扩展代价最下的路径,如果每个代价一致就是宽度优先
假设每条边的代价\(\epsilon\)都为正数且不能任意小,假设最优解路径的代价为\(C^*\)
完备性:有
最优性:有
时间复杂度\(O(b^{C^*+1})\)
空间复杂度\(O(b^{C^*+1})\)
深度受限搜索
宽度优先在空间复杂度方面存在问题,深度优先又有可能选择了一条很长的或无限长的路径
深度受限搜索:执行DFS,但只到预先指定的深度L

迭代加深搜索
解决深度优先和宽度优先的问题
从深度限制 L = 0 开始,我们迭代增加深度限制,对每个深度限制执行深度受限搜索
完备性:有
最优性:有,如果动作代价一致

双向搜索
同时从初始状态向前搜索和从目标状态向后搜索
假设使用的BFS
完备性:有
最优性:有(一致代价)
时空复杂性\(O(b^{d/2})\)
总结

图搜索
图搜索需要考虑重复路径
路径检测
路径检测确保一个节点不同于路径上它的任何祖先节点
环检测
确保得到的后继节点不同于任何先前扩展过的节点
总结

启发式搜索
基本思路是设计一个启发式函数h(n),用于猜测从节点n到达目标节点的代价
贪婪最佳优先搜索
使用h(n)来对边界上的节点进行排序
然而这个方法忽略了达到n的代价,因此这个算法可能会探索那些接近目标但远离初始状态的节点
所以贪婪最佳搜索不是最优的
A*搜索
定义一个评价函数f(n) = g(n)+h(n):
- g(n)表示从初始状态到节点n路径的代价
- h(n)表示从节点n到一个目标节点的代价的启发式
使用f(n)来对边界上的节点进行排序
可采纳性:每个节点的启发式估计小于真实的代价\(h(n) \le h*(n)\)
一致性:\(h(n_1) \le c(n_1->n_2)+h(n_2)\),一致性蕴含可采纳性
时空复杂性:当所有节点的h(n)=0,退化成一致代价搜索,所以时空复杂性与一致代价搜索一样(最差)
可采纳性蕴含最优性,如果只有可采纳性,则环检测不保证最优性,可以记录下以前路径的节点,如果新的路径代价更低,可重新探索
有单调性,则环检测保证最优性

IDA*搜索

决策树
决策树表示一个函数,该函数将属性值向量作为输入,并返回一个”决策“(单个输出值)
- 节点:用属性标记
- 边:用属性值标记
- 叶子:用决策标记
决策树的表示
决策树表示属性值约束的合取的析取

任何的布尔函数都可以写成决策树,也可以通过真值表把表中的每一行对应决策树中的一条路径。
决策树的学习
目的:是为了找到一颗最符合测试样例的决策树
思路:选择一个”最重要“的属性做为(子)树的根,从而不断的递归下去。

信息增益
如何选择一个最重要的属性?
我们使用信息增益的概念,它是用信息论的基本概念-熵来定义的。
熵是对随机变量不确定性的度量:一个只有一个值的随机随机变量没有不确定性,其熵被定义为0;抛一枚硬币具有”1 bit“的熵。
我们定义以概率\(P(V_k)\)取值\(V_k\)的随机变量\(V\)的熵为: \[ H(V) = -\sum_k{P(V_k)log_2P(V_k)} \] 所以以概率q为真的布尔变量的熵为: \[ B(q) = -(qlog_2q+(1-q)log_2(1-q)) \] 对于一个目标属性来说,我们可以把整个训练集当作一个布尔变量,假如这个训练集有p个正例,n个负例,那么该训练集的熵就为 \[ H(GOAL) = B(\frac{p}{p+n}) \] 具有d个不同值的属性A可以将训练集E划分为\(E_1,...,E_d\)
每个子集都有\(p_k\)个正例和\(n_k\)个负例,因此测试属性A之后剩余的熵为: \[ Reminder(A) = \sum_{k=1}^{d}{\frac{p_k+n_k}{p+n}B(\frac{p_k}{p_k+n_k})} \] 对A的测试属性的信息增益是熵的减少: \[ Gain(A) = B(\frac{p}{p+n})-Reminder(A) \] 选择信息增益最大的属性
Gini指数
熵模型拥有大量耗时的对数运算,基尼指数在简化模型的同时还保留了熵模型的优点。
基尼指数反映了从数据集中随机抽取两个样例,其类别标记不一致的概率
如果一个数据集D包含来自n类的样本,那么它的Gini指数为: \[ Gini(D) = \sum_{i=1}^np_i(1-p_i) \] 其中\(p_i\)是类i在D中的概率。
很显然对于决策树来说只有两类”Yes“或”No“,所以: \[ Gini(D) = 2p(1-p) \] p为其中正例的比例
假设属性A的取值将D划分为\(D_1,...,Dm\) \[ Gini(D|A) = \sum_{i=1}^{m}\frac{D_i}{D}Gini(D_i) \] 选择具有最小基尼指数的属性作为节点即可