计算机图形学笔记
变换
透视投影矩阵
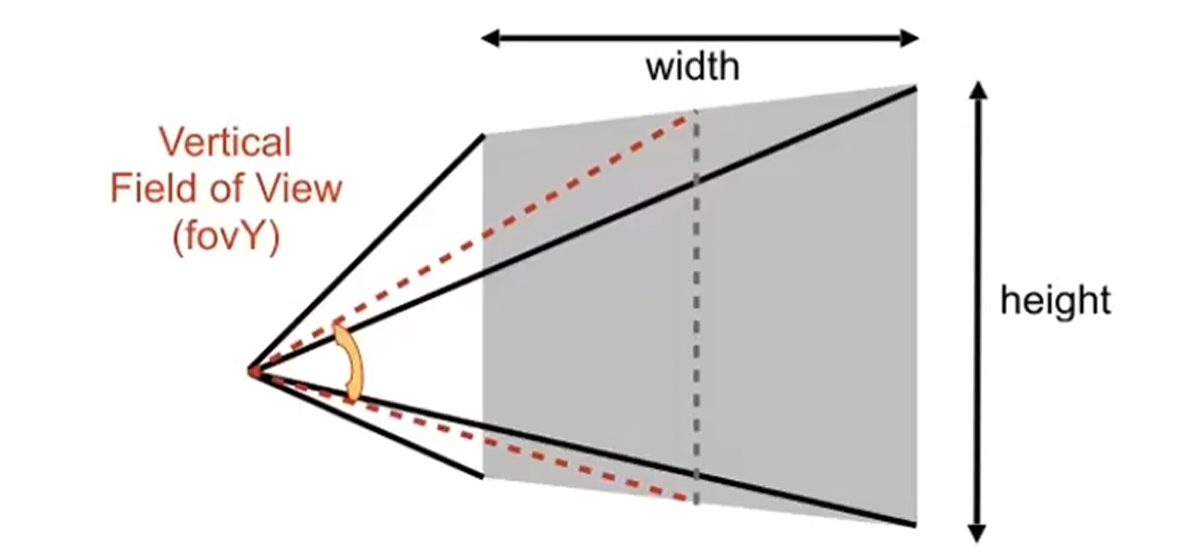
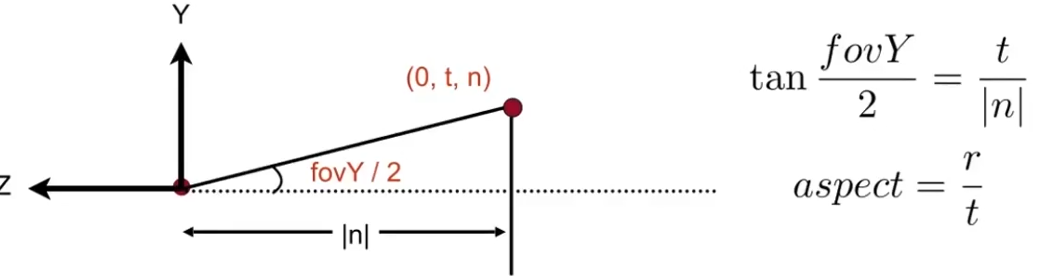
光栅化
屏幕:二维数组
- 像素(x,y)

转换到屏幕空间(先不管z轴)

抗锯齿(反走样)
采样会产生一系列问题,比如说锯齿,摩尔纹
这些问题产生的本质原因都是因为:信号变化太快,而采样无法跟上
走样:同一组采样,但是他的信号函数可以完全不一样
采样:在时域上是乘积,在频域上就是卷积。如果采样太稀疏了,频率的重复就会重叠
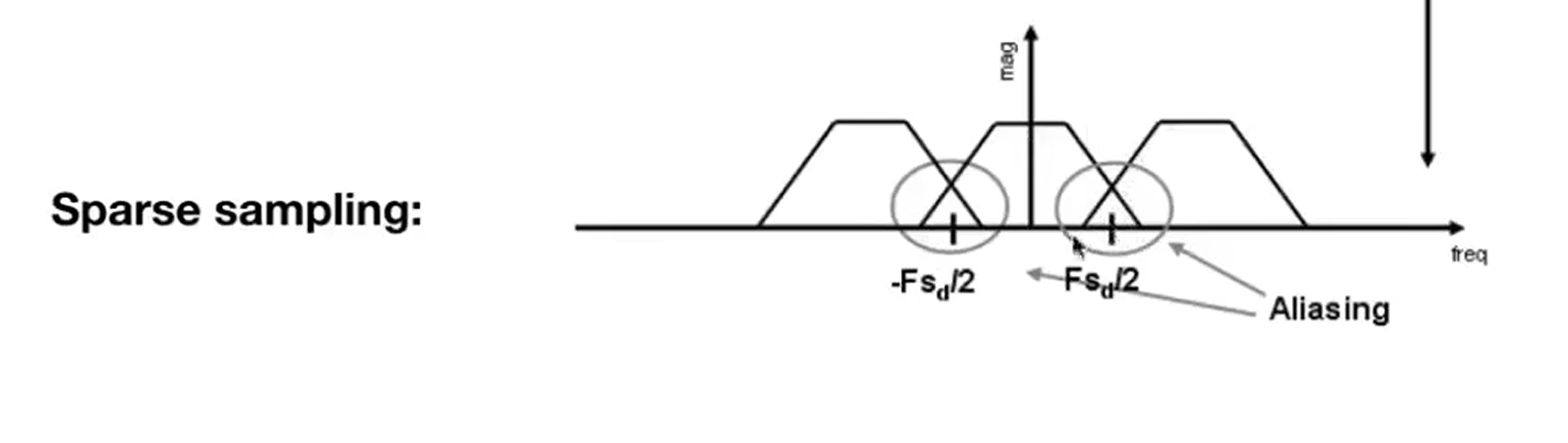
解决走样问题:
增加采样率(这不是反走样)
反走样:
- 先模糊(低通滤波)(用滤波器进行卷积),由下图可以看出频域上不再重叠
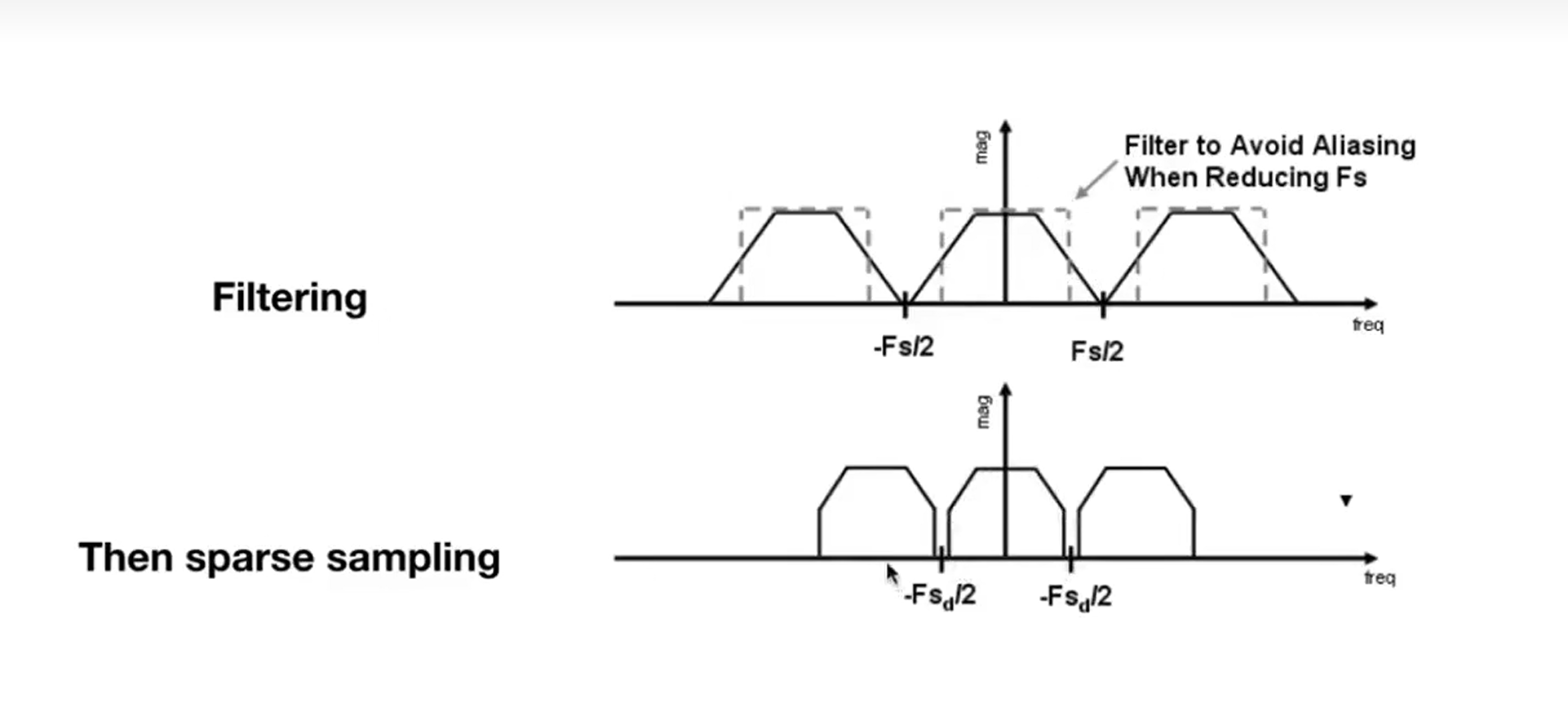
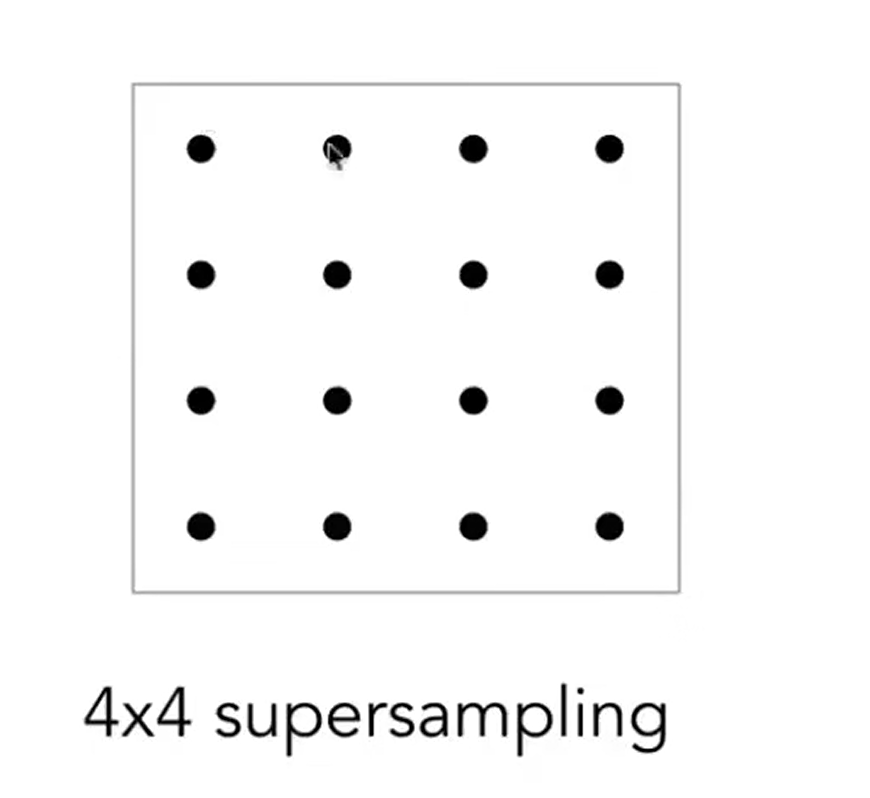
Supersample:
- 把一个像素分成更多的小的点,来近似一个像素的平均
Z-buffer
图像生成的过程中,同时会生成一个表示深度的图像

算法如下:

着色
对不同的物体映射不同的材质
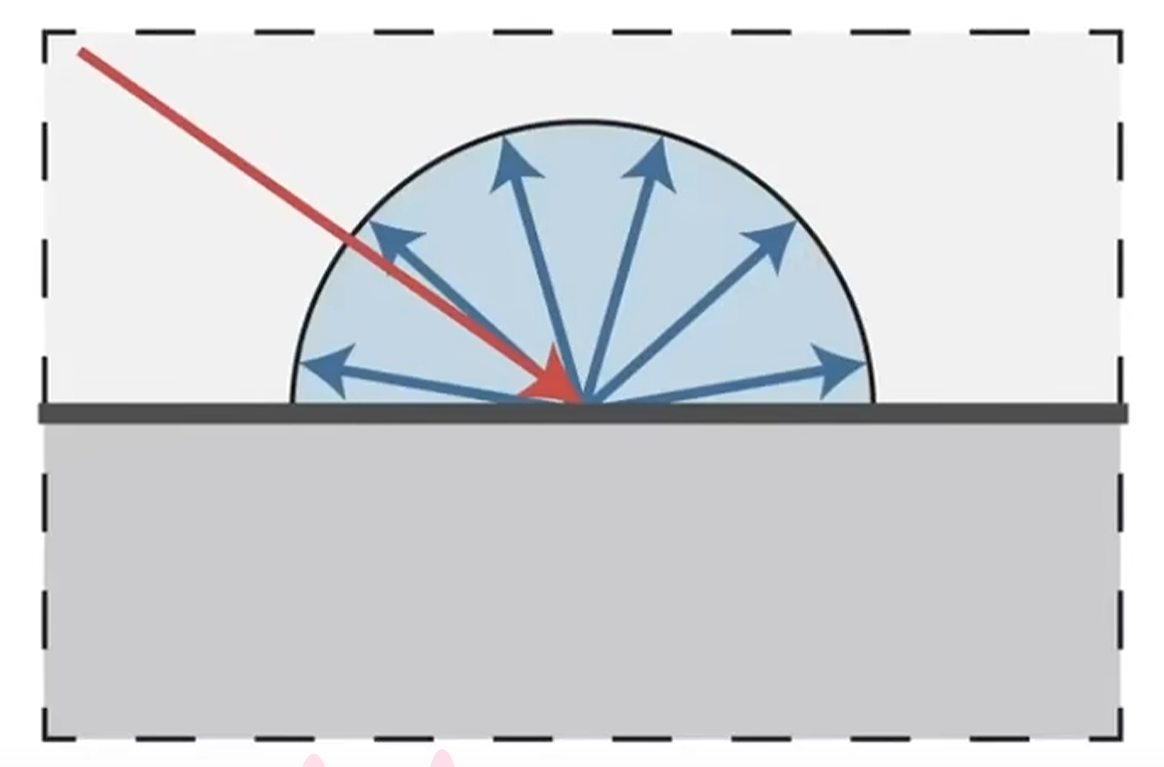
漫反射
- 漫反射:光线会被均匀的发射到各个方向上去
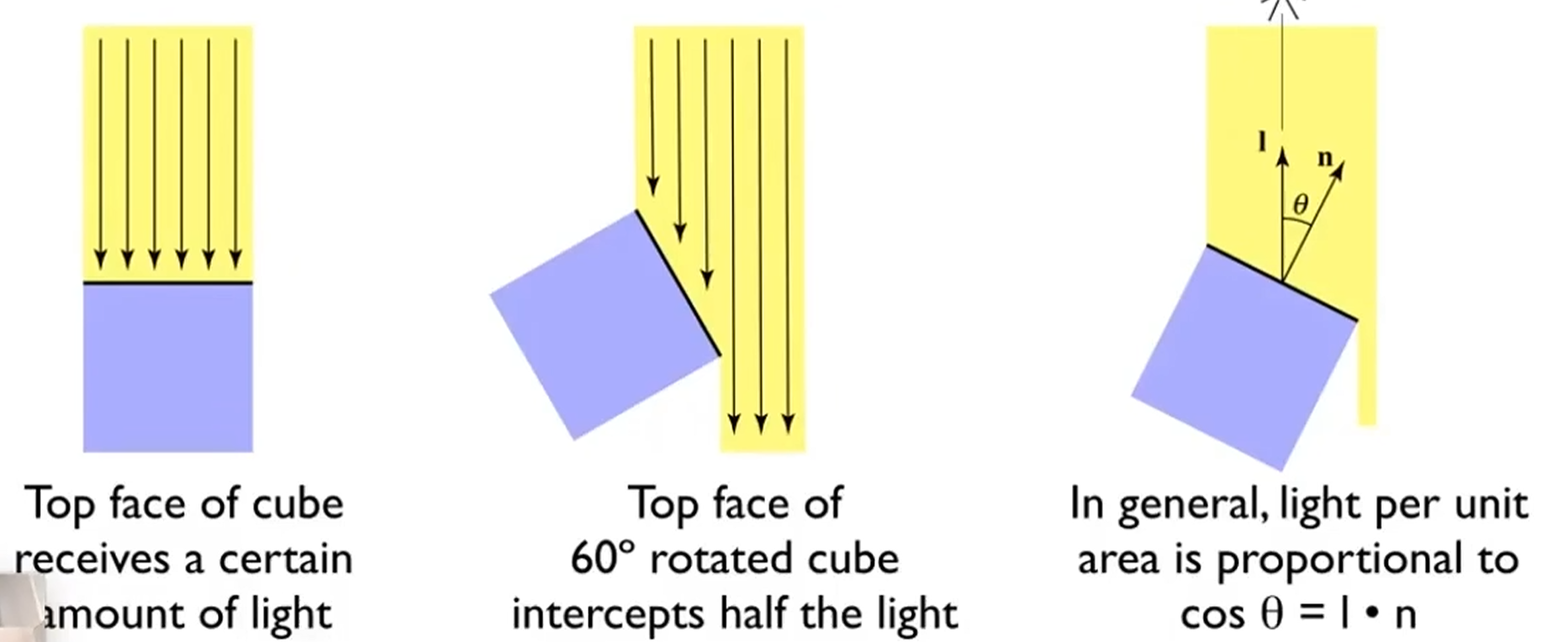
- 着色点接收到的光照能力与光线方向和法线的余弦成正比
- 点光源的光的强度随距离的平方成反比
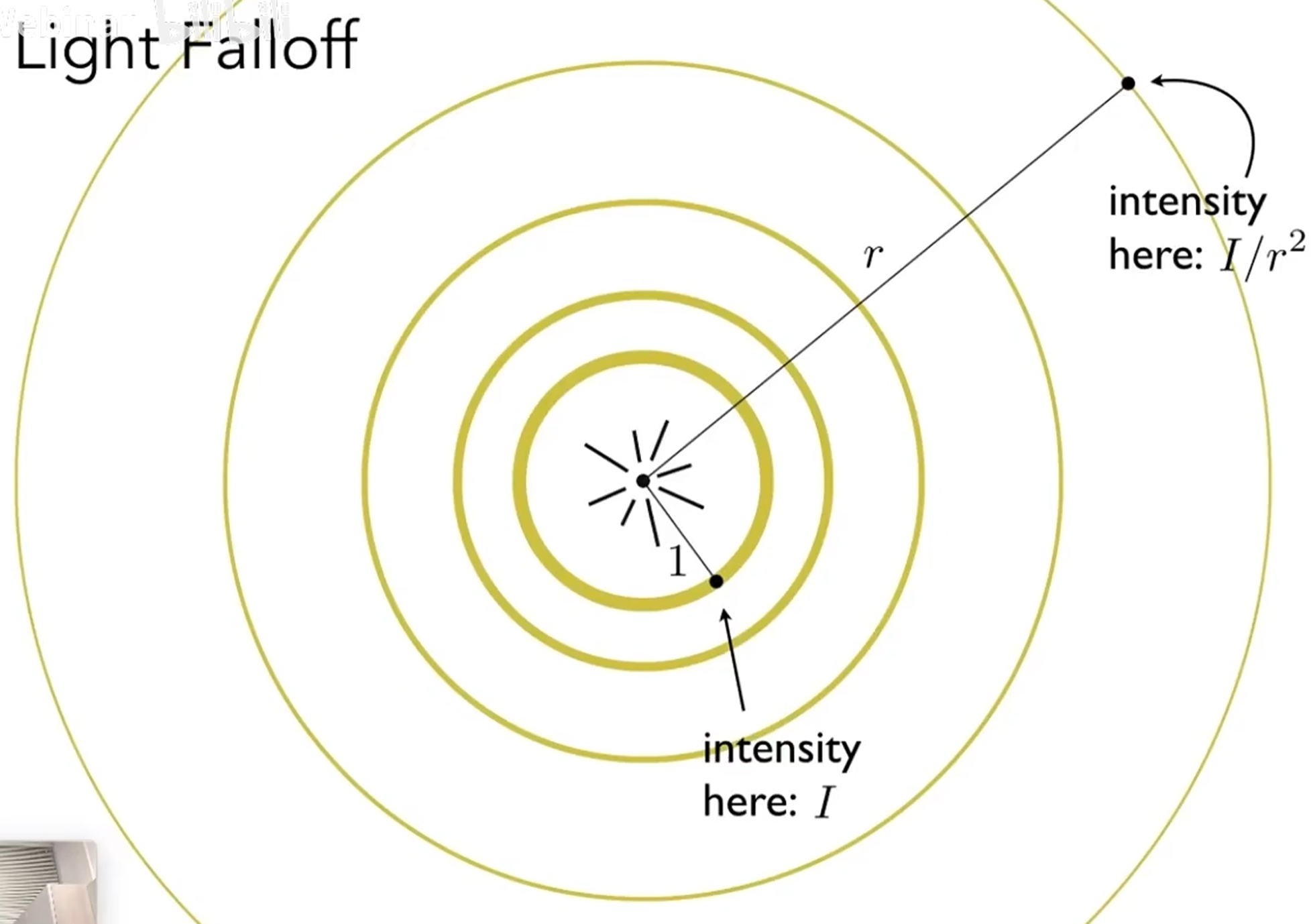
因此可以得到漫反射的光的计算公式如下:\(K_d\)是漫反射系数,表示物体吸收多少能量。\(n,l\)都是方向向量即单位向量
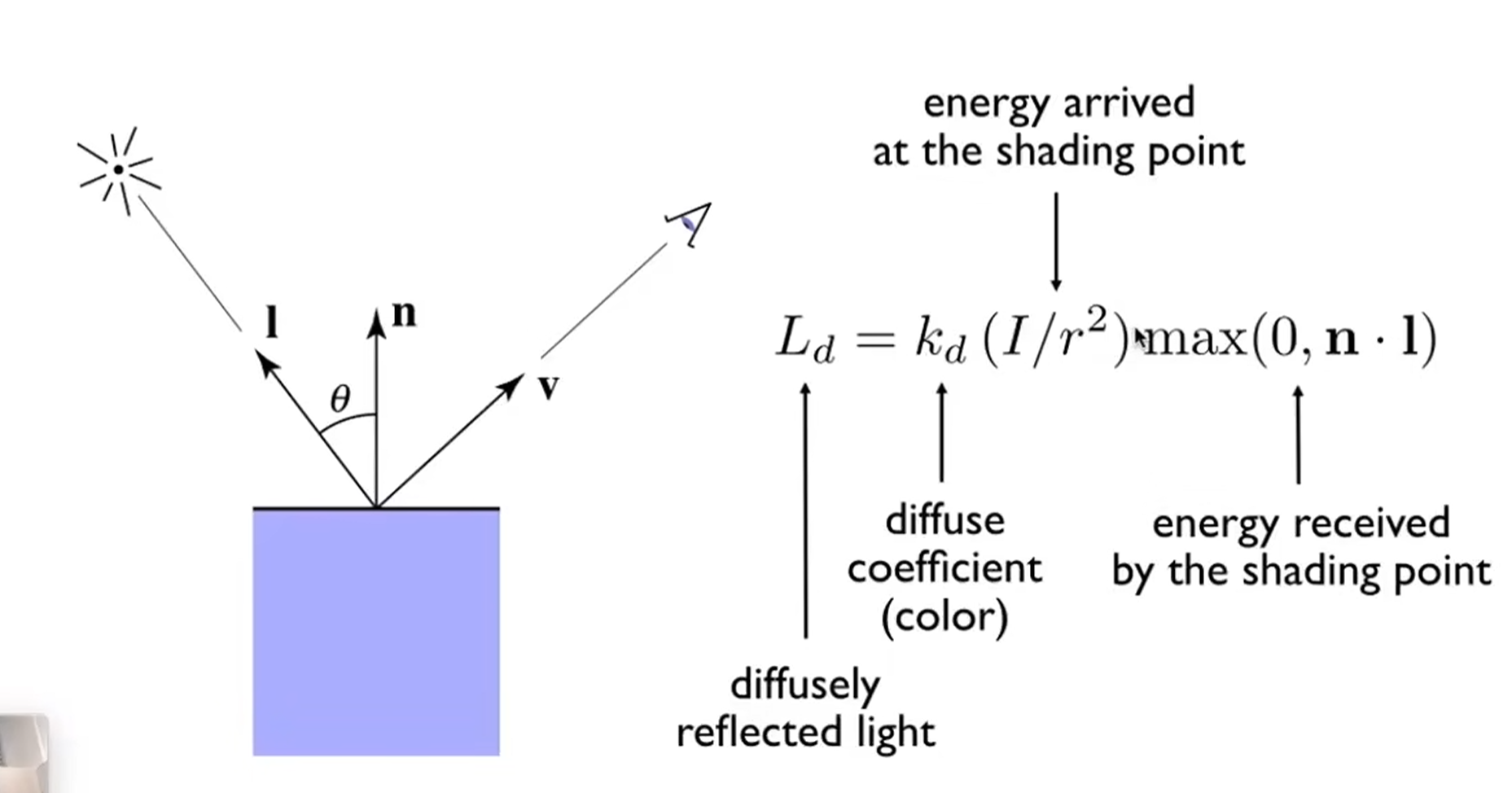
镜面反射
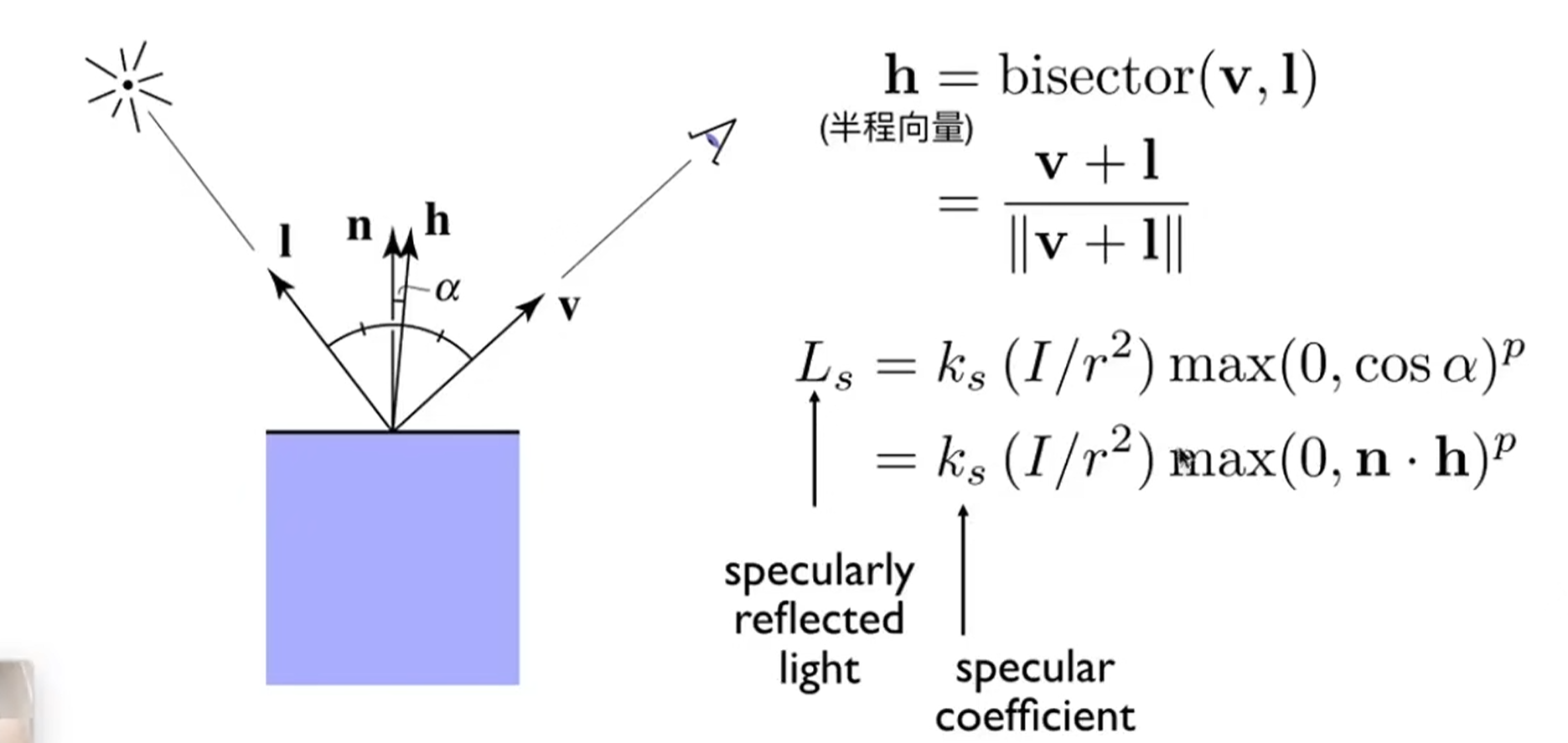
环境光照像
和入射光线以及观测方向都没关系
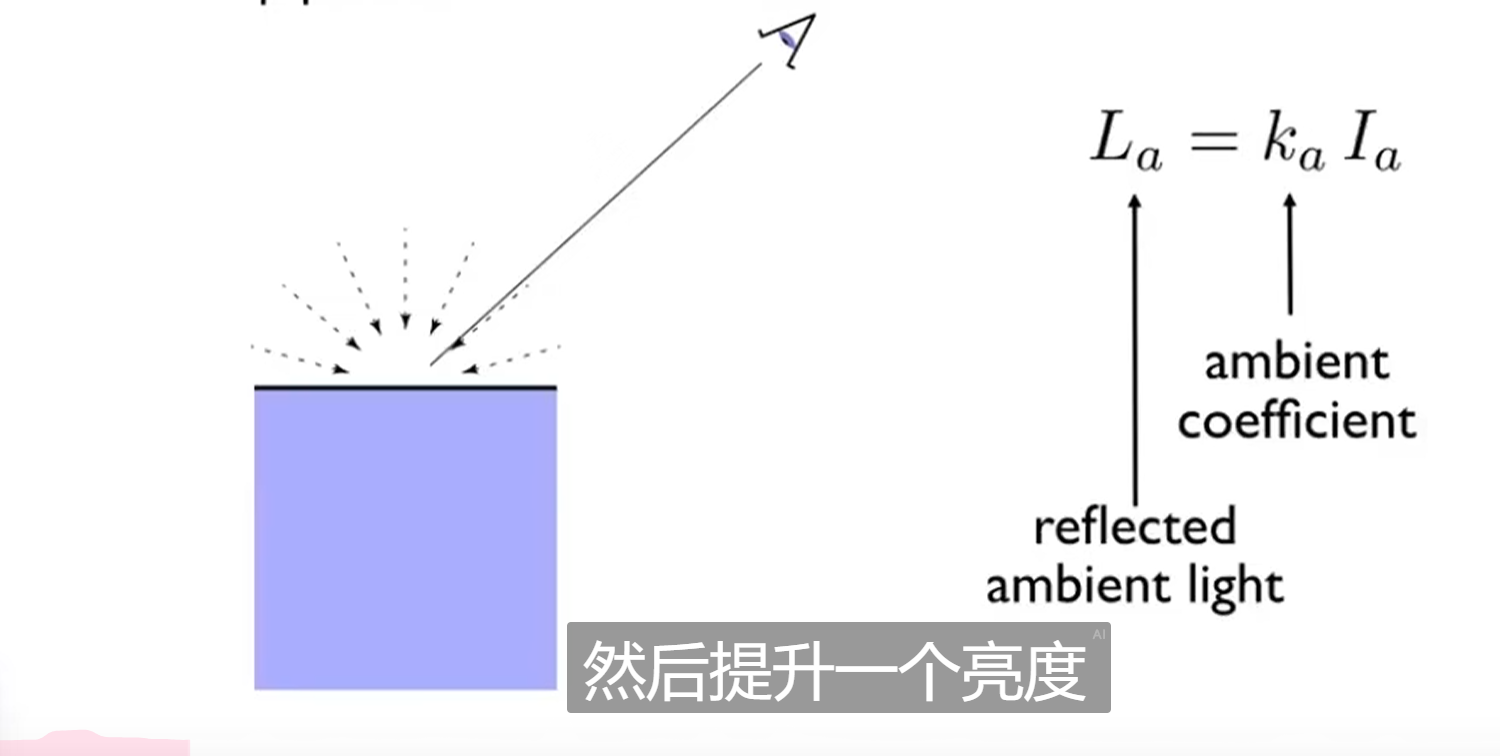
Blinn Phong反射模型

纹理映射
纹理就是一张图,把这张图蒙在三维物体上,就是纹理映射
纹理坐标系,三角形的每一个顶点都对应一个纹理坐标系上的点
重心坐标
为什么要做差值:
- 很多操作需要对三角形做,我们需要使三角形内部平滑过渡
重心坐标:
- 任何一个三角形内部的一个点的坐标都可以用三角形顶点的线性组合来表示,如下图:
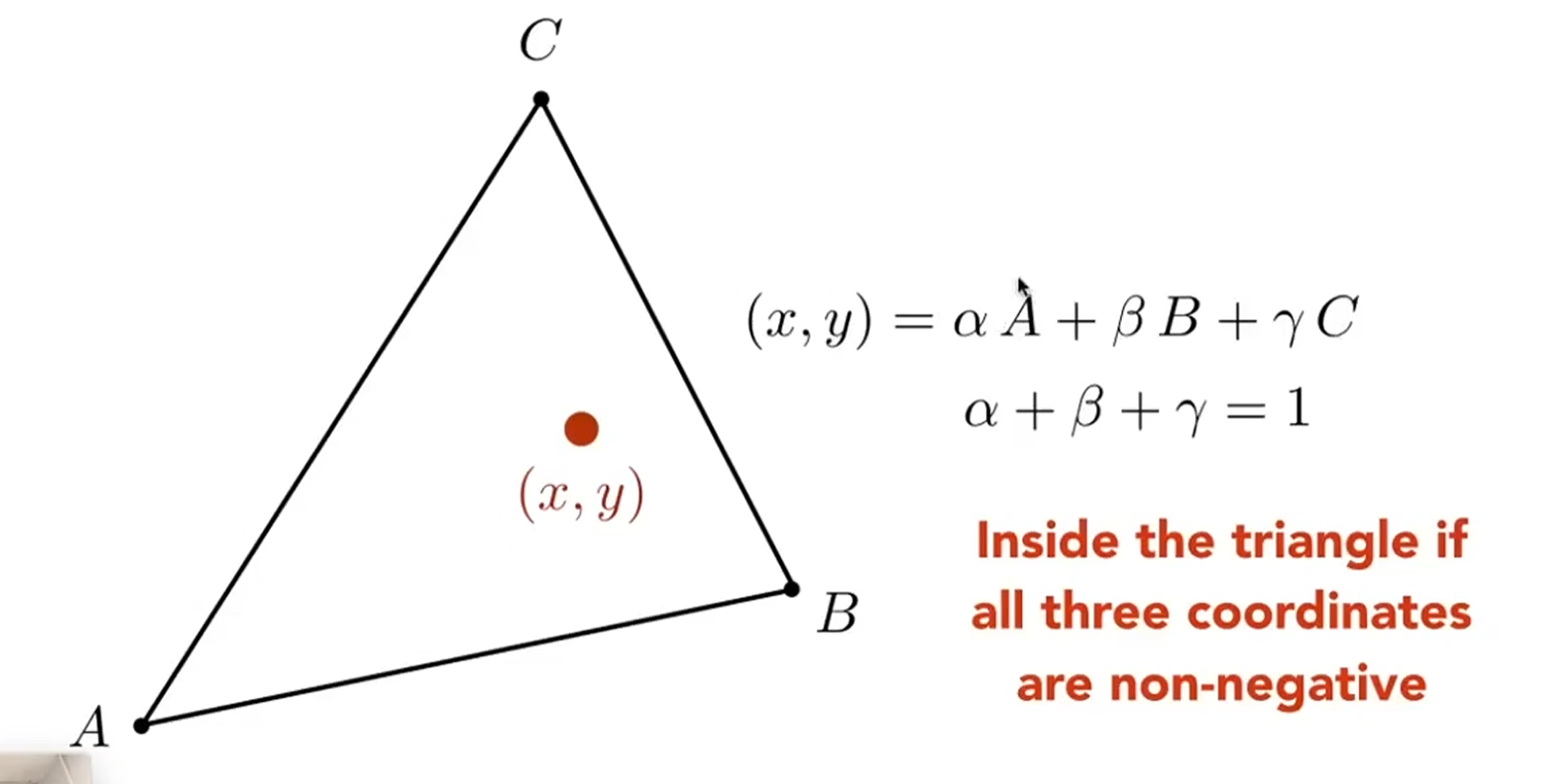
那么重心坐标为:
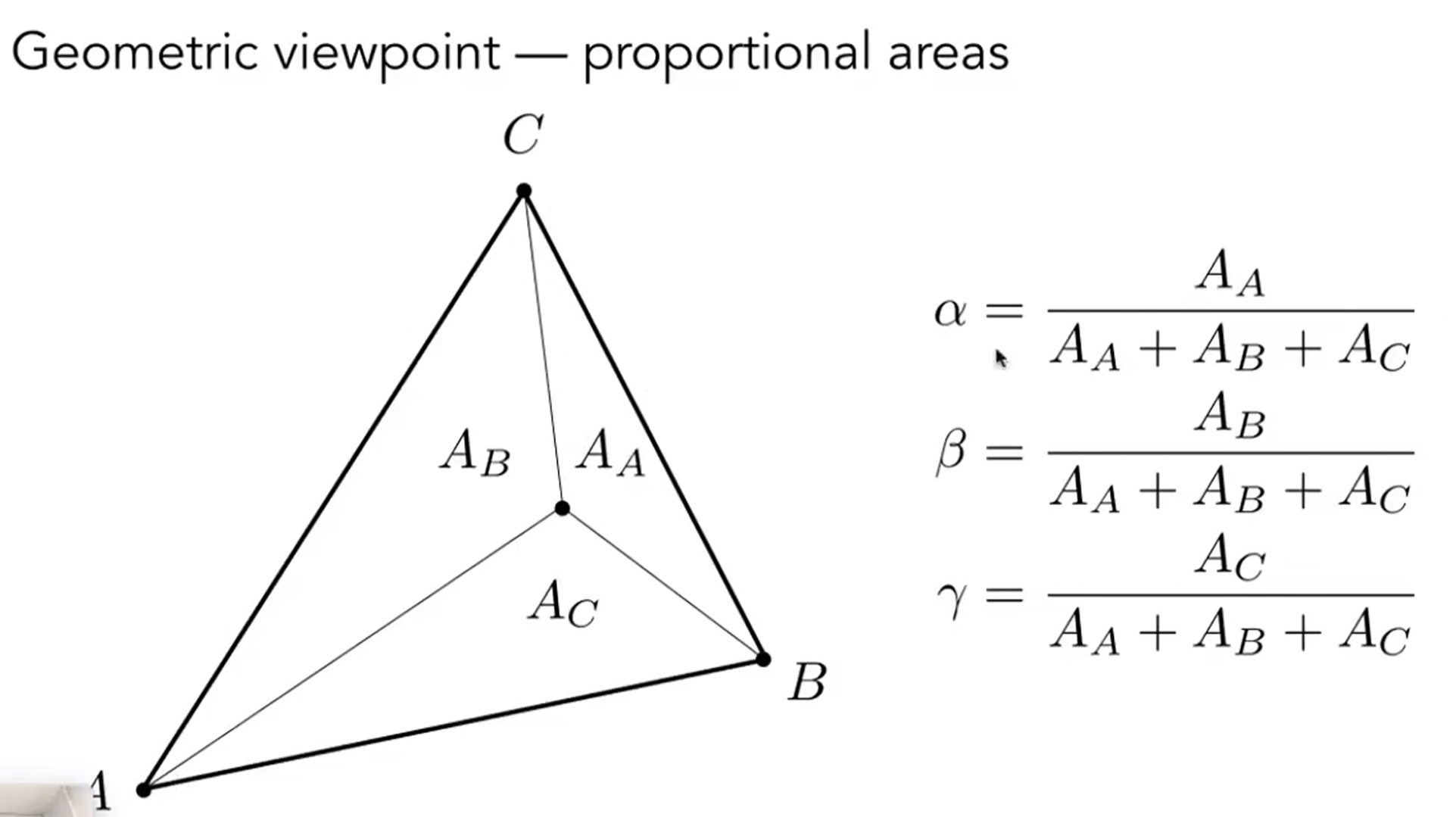
可以简化得
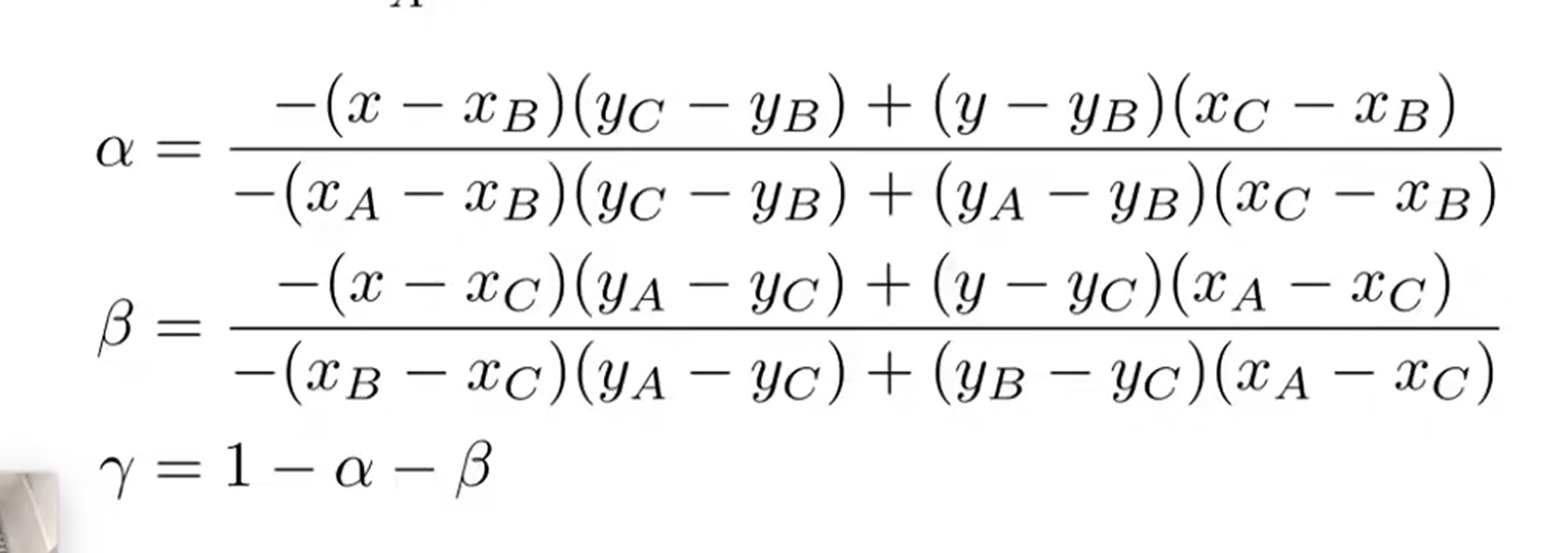
注意:现在三维空间中做插值,再投影到屏幕空间上。
纹理放大
纹理太小了,很大像素被映射到一个texel上

双线性插值:
一个像素被映射到纹理坐标上,并不是整数,这样就需要一个插值,否则就是选择一个最近点进行近似,就像上图坐标的图的情况。
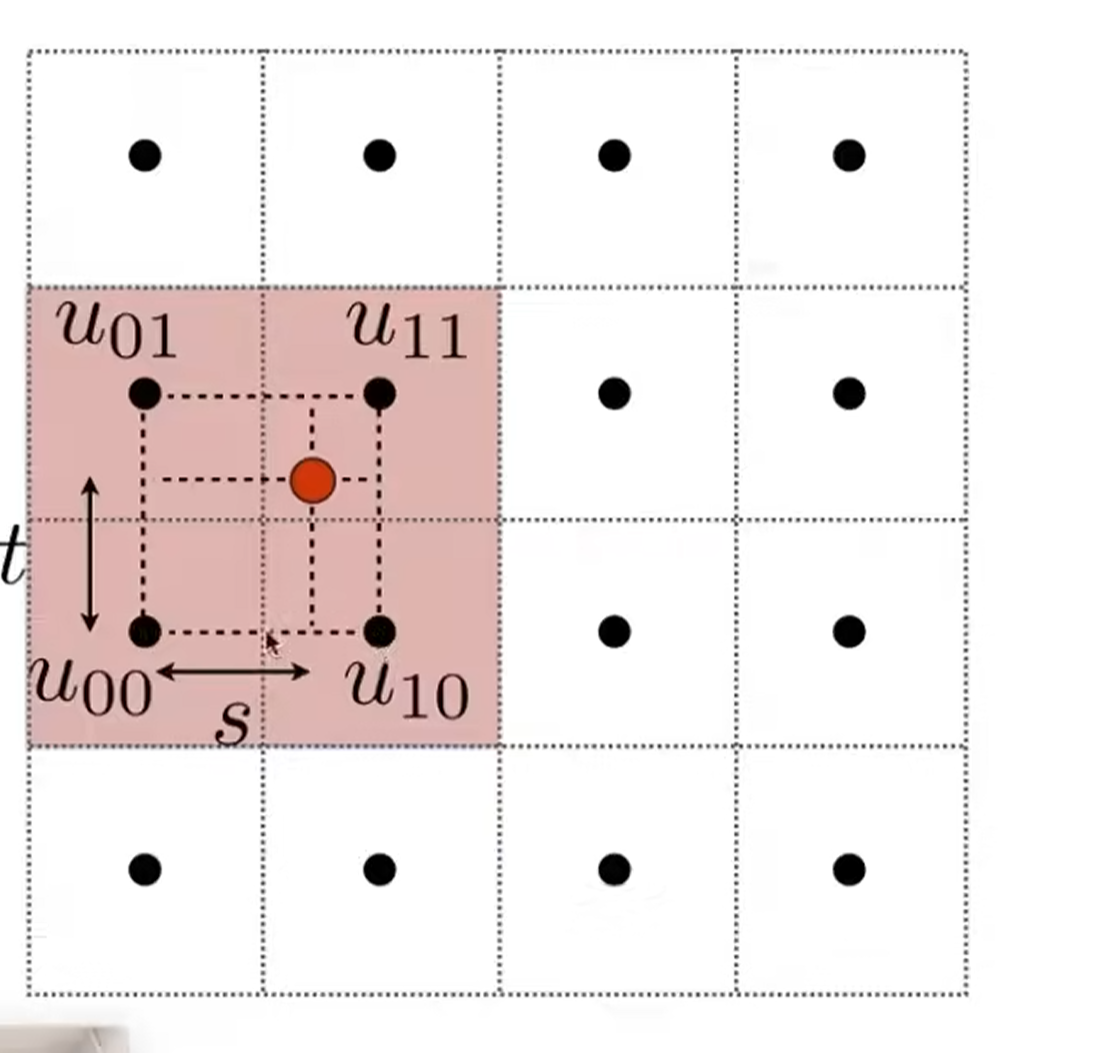
按照如下的方法进行插值:

如果纹理过大,会产生锯齿(一个像素包含了一大块纹理)
除了反走样之外的解决方法:
mipmap:允许得到纹理一个范围内的平均值,如下所示,可以提前得到平均值
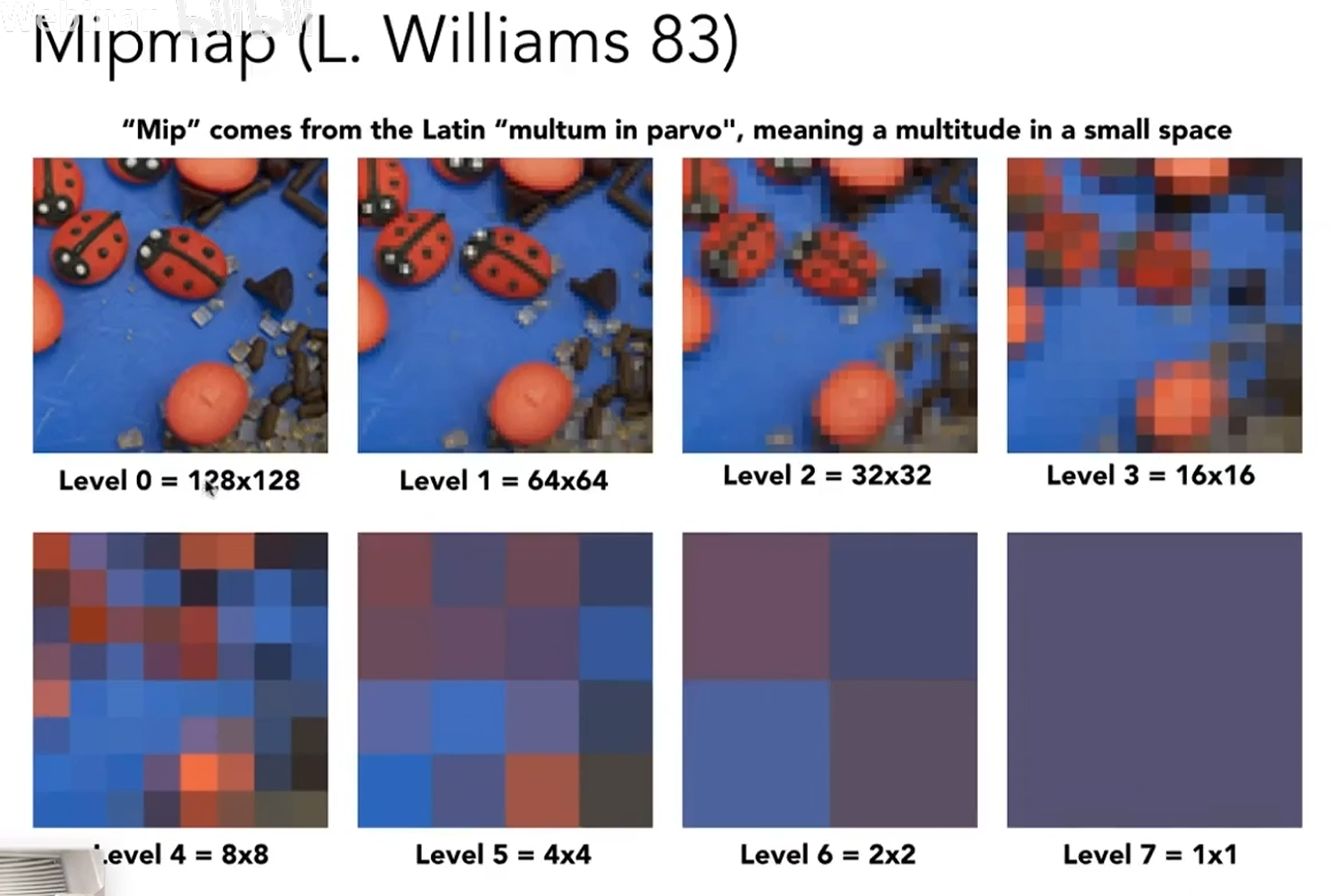
当把一个像素包含的纹理,可以近似为一个正方形,如果这个正方形是4*4大小的,那我们可以在level 2的纹理上找到。
如果我们需要level 1.8的则需要再做插值
mipmap存在一些问题,比如映射在纹理空间上不是正方形,如下图
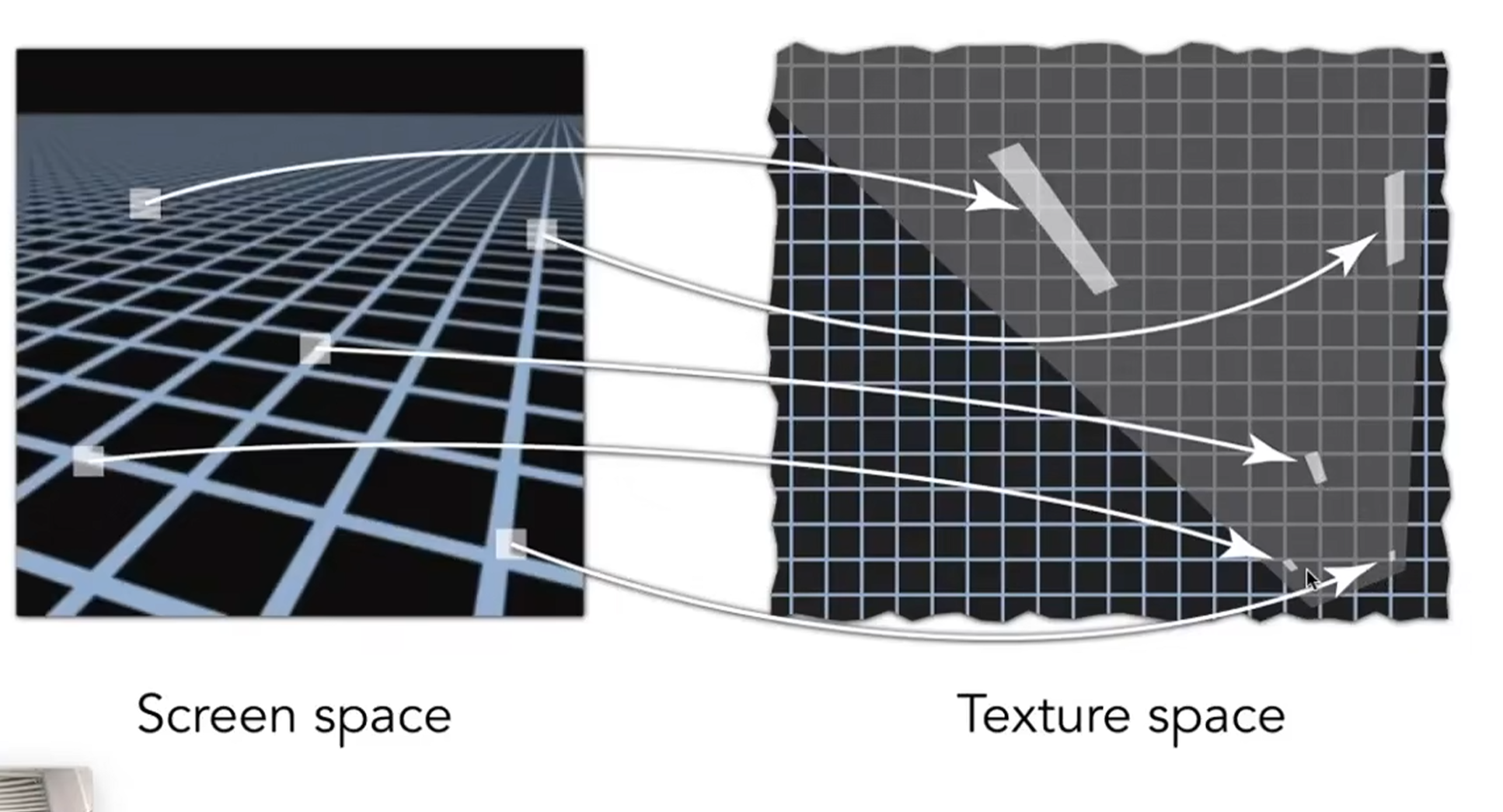
可以用各项异性过滤(矩形)解决一点,还有ewa过滤(圆形)
纹理应用
纹理可以用来表示环境光
cuba map:用正方体
凹凸贴图:不改变几何结构,而是贴一张图表现凹凸的结构
用于记录之前已经进行过的计算
10节:38分