doovvv
0%

算法刷题记录

Posted on Edited on Valine:

some record about leetcode.

LC 560.和为K的子数组

思路

滑动窗口

由于该数组存在负数，所以滑动窗口不可行

此处只为记录一下滑动窗口大致思路：
由于题目是求连续非空序列的个数，所以自然而然联想到滑动窗口。
维护一个滑动窗口内数目的和sum：

  • 当sum < k 时，滑动窗口的右边界向右滑动一个单位
  • 当sum > k 时，滑动窗口的左边界向右滑动一个单位
  • 当sum == k 时，计数器加一

如果题目没要求序列连续的话，应该可以先排序再用滑动窗口

哈希+前缀和

一个下标较大的前缀和减去一个下标较小的前缀和就为一个连续序列的和。
假设有两个前缀和：pre[i],pre[j]，并且 0 <= j < i < n.
所以连续序列的和就为k = pre[i] - pre[j]。该序列以下标为i的元素结尾，所以序列和为k，并且以下标为i的元素结尾的序列的个数就是pre[j]的个数。 所以我们只需要遍历i，然后统计对应pre[j]的个数，最终的个数即为答案。
具体做法为：从左到右，遍历一遍数组，即增加i的值，在这个过程中，把前缀和放入哈希表中，前缀和为键，每当一个前缀和的键出现，就对该前缀和对应的值加一。这样便可以得到相应pre[j]的个数，同时又遍历了i。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        //sort(nums.begin(),nums.end());
        int pre = 0;
        int ans = 0;
        map<int,int> hash;
        hash[0] = 1; //即j = 0时的前缀和
        for (int i = 0;i<nums.size();i++){
            pre += nums[i];
            int pre_j = pre - k;
            if(hash.find(pre_j) != hash.end()){
                    ans += hash[pre_j];
            }
            if(hash.find(pre) == hash.end()){
                hash[pre] = 1;
            }
            else{
                hash[pre]++;
            }
        }
        return ans;
    }
};

LC 76.最小覆盖子串

思路

该题使用滑动窗口很简单，不过多赘述

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
public:
    bool is_cover(map<char,int>& hash){
        bool flag = true;
        for(auto key_value:hash){
            if(key_value.second > 0){
                flag = false;
                break;
            }
        }
        return flag;
    }
    string minWindow(string s, string t) {
        map<char,int> hash;
        for(int i = 0;i<t.length();i++){
            if(hash.find(t[i]) == hash.end()){
                hash[t[i]] = 1;
            }
            else{
                hash[t[i]] += 1;
            }
        }
        int flag = 0;
        string ans = "";
        int first_time = 1;
        int i = 0,j = 0;
        while(i < s.length() && j<=i || (i == s.length() && flag == 1)){
            if(flag == 0){
                if(hash.find(s[i]) != hash.end()){
                    hash[s[i]]--;
                    if(is_cover(hash)){
                        flag = 1;
                    }
                }
                i++;
            }
            if(flag == 1){
                if(hash.find(s[j]) != hash.end()){
                    hash[s[j]]++;
                    if(!is_cover(hash)){
                        string temp = s.substr(j,i-j);
                        flag = 0;
                        if(temp.length() < ans.length() || first_time){
                            //cout<<j<<" ";
                            ans = temp;
                            first_time = 0;
                        }
                    }
                }
                j++;
            }
        } 
        return ans;
    }
};

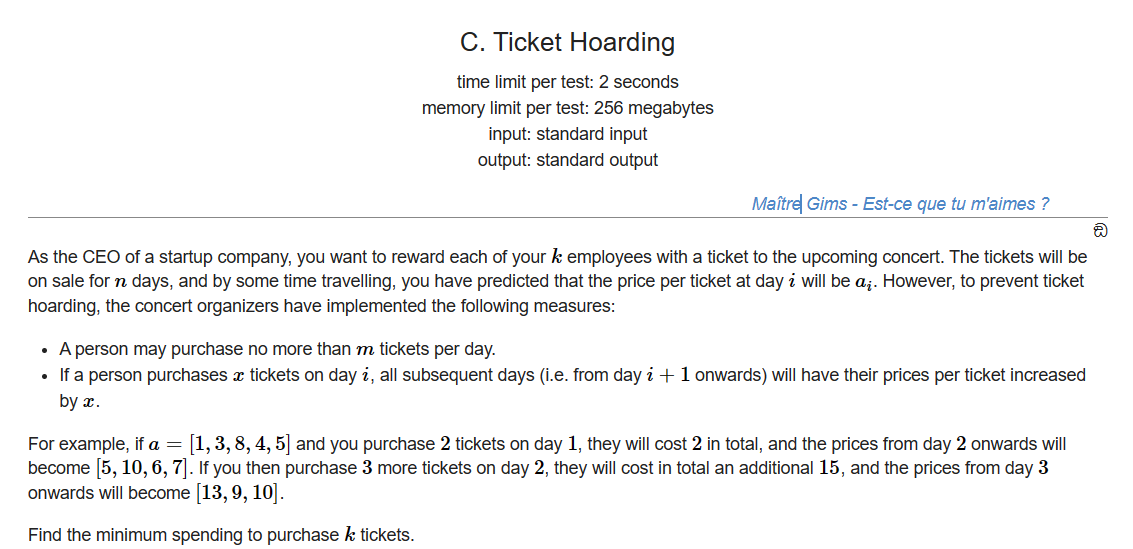
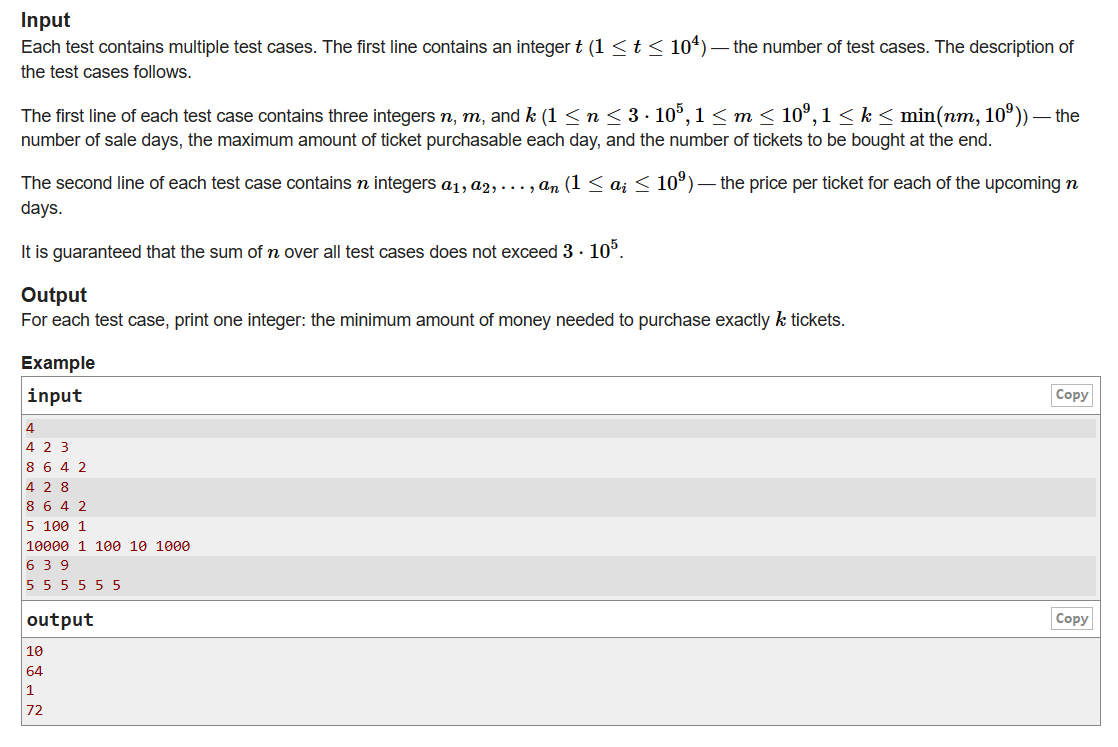
Codeforces Global Round 25(C.Ticket Hoarding)


  • 题目链接

    思路

    显然，当价格较小的票在较后的时间里时，只需要贪心的选择较小的票即可。
    当价格较小的票在价格较大的票之前时，我们可能需要思考如何分配票数。
    我们令T1表示价格较小的票的价格，N1表示它的票数，T2、N2同理
    T1和T2的位置关系也就不重要了，因为N1T1+N2（T2+N1）= N2T2+N1（T1+N2）。
    并且显然当T1位置靠后时，优先多选择T1，然而只要N1和N2确定，位置关系不影响结果，所以只要排序之后，贪心的选择最小的票即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
    int t;
    cin>>t;
    while(t--){
        int n,m,k;
        cin>>n>>m>>k;
        vector<int> nums;
        for(int i = 0;i<n;i++){
            int num;
            cin>>num;
            nums.push_back(num);
        }
        sort(nums.begin(),nums.end());
        int count = 0;
        int ans = 0;
        int cnt = 0;
        int index = 0;
        while(count < k){
            int temp = min(m,k);
            int ticket = min(temp,k-count);
            count += ticket;
            ans += ticket*(nums[index]+cnt);
            cnt += ticket;
            index++;
        }
        
        cout<<ans<<endl;
    }
}

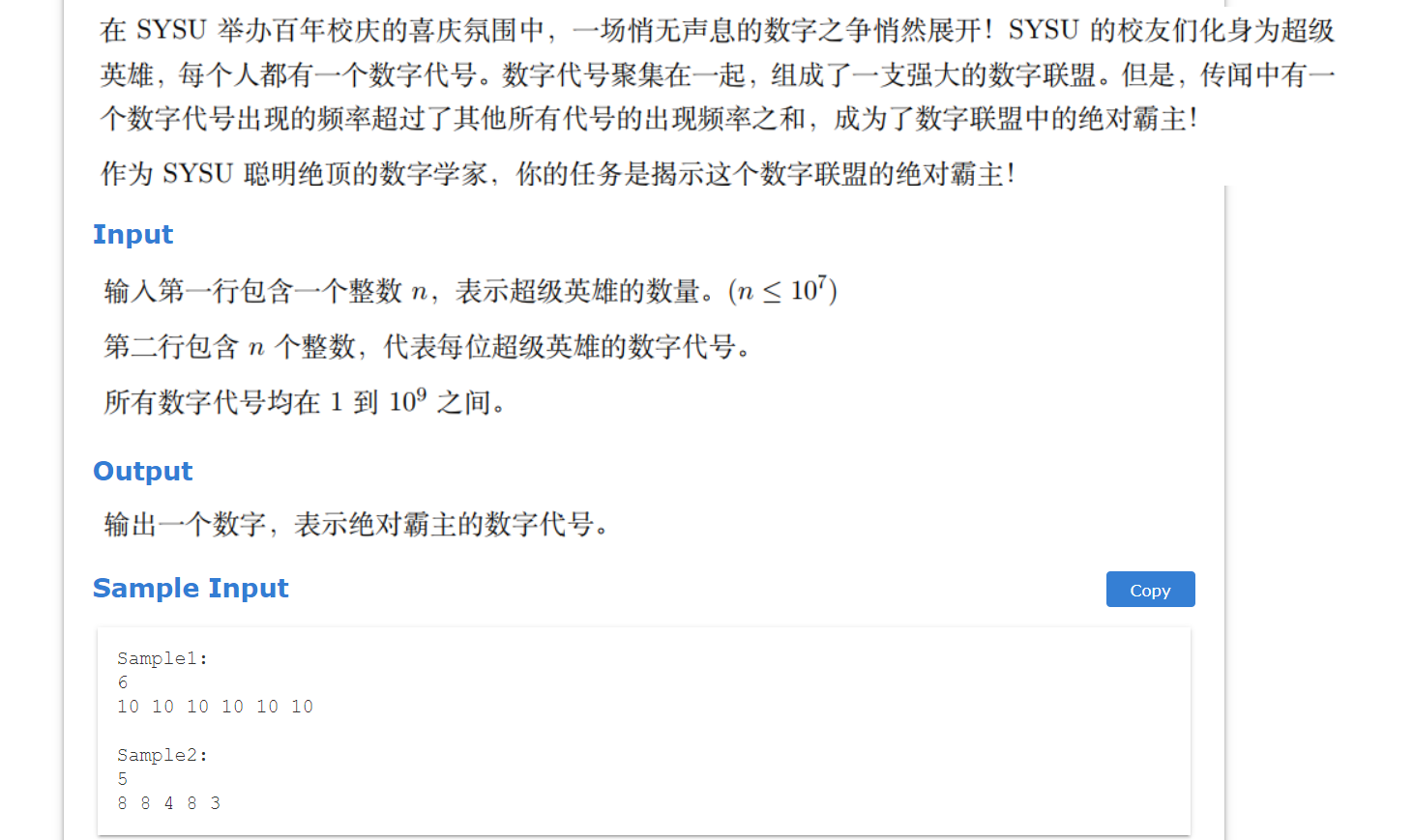
NVCPC 2024 绝对霸主

题目

image-20240430121247754

思路

求绝对众数，用摩尔投票算法。

绝对众数：在一个集合中，如果一个元素的出现次数比其他所有元素的出现次数之和还多，那么就称它为这个集合的绝对众数。等价地说，绝对众数的出现次数大于总元素数的一半

摩尔投票的过程：维护一个m，表示当前的众数，然后维护一个cnt，表示票数。遍历每个数，对每个数y

  • 如果cnt=0，则修改m = y
  • 若m = y，cnt++
  • 若m != y，cnt—

摩尔投票的算法思想就是利用抵消，因为绝对众数的特性，最后的m一定是绝对众数，利用摩尔投票可以大大减少内存的开销。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<bits/stdc++.h>
using namespace std;
int main(){
    int n;
    cin>>n;
    int m,cnt = 0;
    for(int i = 0;i<n;i++){
        int num;
        cin>>num;
        if(cnt == 0){
            m = num;
        }
        if(m == num){
            cnt++;
        }
        else{
            cnt--;
        }
    }
    cout<<m;
}

Cf Round 944 H

题目

image-20240513165505600

思路

这是2-sat问题，需要转化为图论问题求强连通分量。在此顺便记录一下tarjan求强连通分量的模板。

2−sat 问题 大概 就是给定一串布尔变量，每个变量只可以为真 (1) 或假 (0)，并给出一系列约束变量的条件，要求回答关于满足以上条件的布尔序列的各种信息.

2-sat子句：形如 $ a\or b $ ，子句可以建边-a -> b和-b -> a，可以理解为如果期中一个变量为负，另一个变量一定为正。

此题可以把每一列看成3个2-sat子句，因为每一列三个变量中，至少要有两个为真，所以每两个变量都是一个2-say子句

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 20010;
const int MAXM = 50010;
struct Edge{
    int to,next;
}edge[MAXM];
int head[MAXN],tot;
int Low[MAXN],DFN[MAXN],Stack[MAXN],Belong[MAXN];
int Index,top;
int scc;//强连通分量的个数
bool Instack[MAXN];
int num[MAXN];//各个强连通分量包含点的个数，数组编号 1 ∼ scc
void addedge(int u,int v){
    edge[tot].to = v;edge[tot].next = head[u];head[u] = tot++;
}
void Tarjan(int u){
    int v;
    Low[u] = DFN[u] = ++Index;
    Stack[top++] = u;
    Instack[u] = true;
    for(int i = head[u];i != -1;i = edge[i].next){
        v = edge[i].to;
        if( !DFN[v] ){
            Tarjan(v);
            if( Low[u] > Low[v] )Low[u] = Low[v];
        }
        else if(Instack[v] && Low[u] > DFN[v])
            Low[u] = DFN[v];
    }
    if(Low[u] == DFN[u]){
        scc++;
        do{
            v = Stack[--top];
            Instack[v] = false;
            Belong[v] = scc;
            num[scc]++;
        }
        while( v != u);
    }
}
void solve(int N){
    memset(DFN,0,sizeof(DFN));
    memset(Instack,false,sizeof(Instack));
    memset(num,0,sizeof(num));
    Index = scc = top = 0;
    for(int i = 1;i <= N;i++)
        if(!DFN[i])
            Tarjan(i);
}
void init(){
    tot = 0;
    memset(head,-1,sizeof(head));
}
signed main(){
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        init();
        vector<vector<int>> mat;
        for(int i = 0;i<3;i++){
            vector<int> row;
            for(int j = 0;j<n;j++){
                int num;
                cin>>num;
                if(num < 0){
                    num = -num+n;
                }
                row.push_back(num);
            }
            mat.push_back(row);
        }
        for(int i = 0;i<n;i++){
            for(int j = 0;j<3;j++){
                for(int k = 0;k<3;k++){
                    if(j == k){
                        continue;
                    }
                    if(mat[j][i] > n){
                        addedge(mat[j][i]-n,mat[k][i]);
                    }
                    else{
                        addedge(mat[j][i]+n,mat[k][i]);
                    }
                }
            }
        }
        solve(2*n);
        bool flag = false;
        for(int i = 1;i<=n;i++){
            if(Belong[i+n] == Belong[i]){
                cout<<"No"<<endl;
                flag = true;
                break;
            }
        }
        if(flag == false){
            cout<<"Yes"<<endl;
        }
    }
}


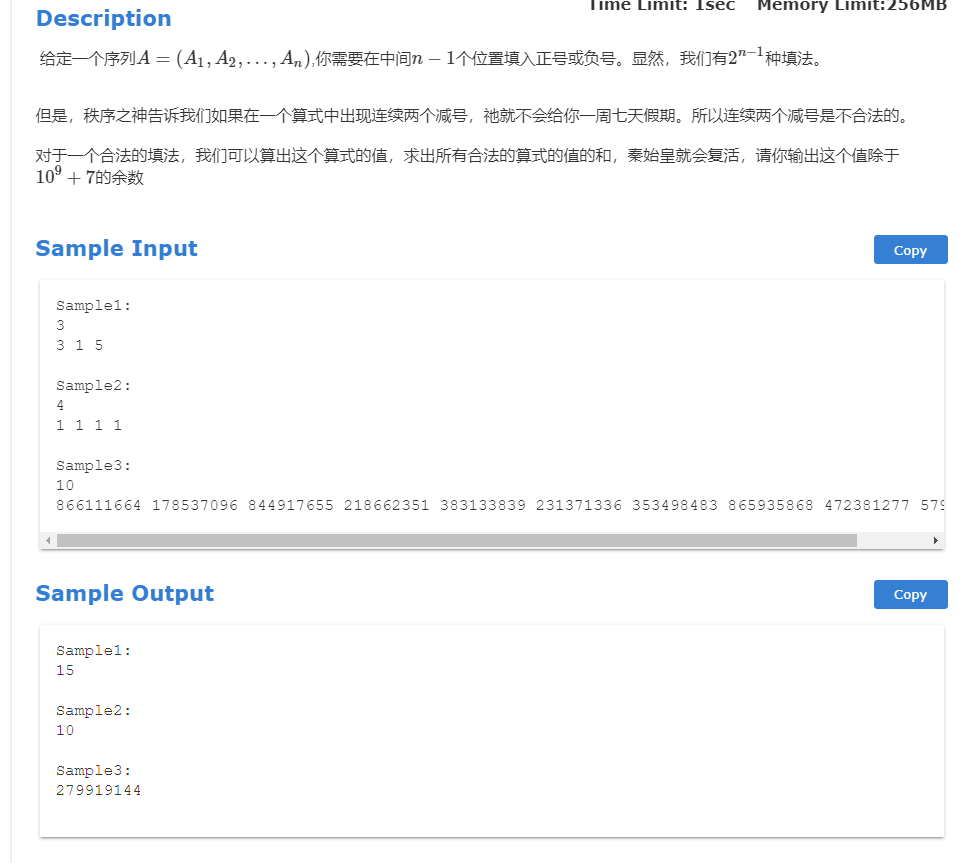
ACMM周赛第一场 T3

题目

image-20240514131521116

思路

本题暴力会超时。

可以单独对每个数字思考，即每个的数字的正数会有多少个和负数有多少个。

假定前i-1个数的填法数量假如为$f{i-1}$，假如第i个数字为正号的数量也为$f{i-1}$，那为负号的数量也就为$f{i-2}$。但是实际情况是第个数字的数量还要考虑大于i的数字的填法数。所以第i个数字为正号的数量为$f{i-1} f{n-i} $，同理得负号的数量为$f{i-2} f_{n-i-1}$。注意，由于第一个数不需要填正负号，所以计算大于i的数字的填法数时下标要加1

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define MAXN 1000000007
int ans;
signed main(){
    int n;
    cin>>n;
    int ans = 0;
    vector<int> f(n+1);
    f[0] = 1;
    f[1] = 1;
    for(int i = 2;i<=n;i++){
        f[i] = (f[i-1] + f[i-2]) % MAXN;
    }
    for(int i = 1;i<=n;i++){
        int num;
        cin>>num;
        if(i == 1){
            ans = (ans + f[n]*num) % MAXN;
        }
        else{
            ans =(ans + f[i-1]*f[n-i+1]%MAXN*num)%MAXN;
            ans = (ans- f[i-2]*f[n-i]%MAXN*num%MAXN+MAXN)%MAXN;
        }
    }
    cout<<ans;
}

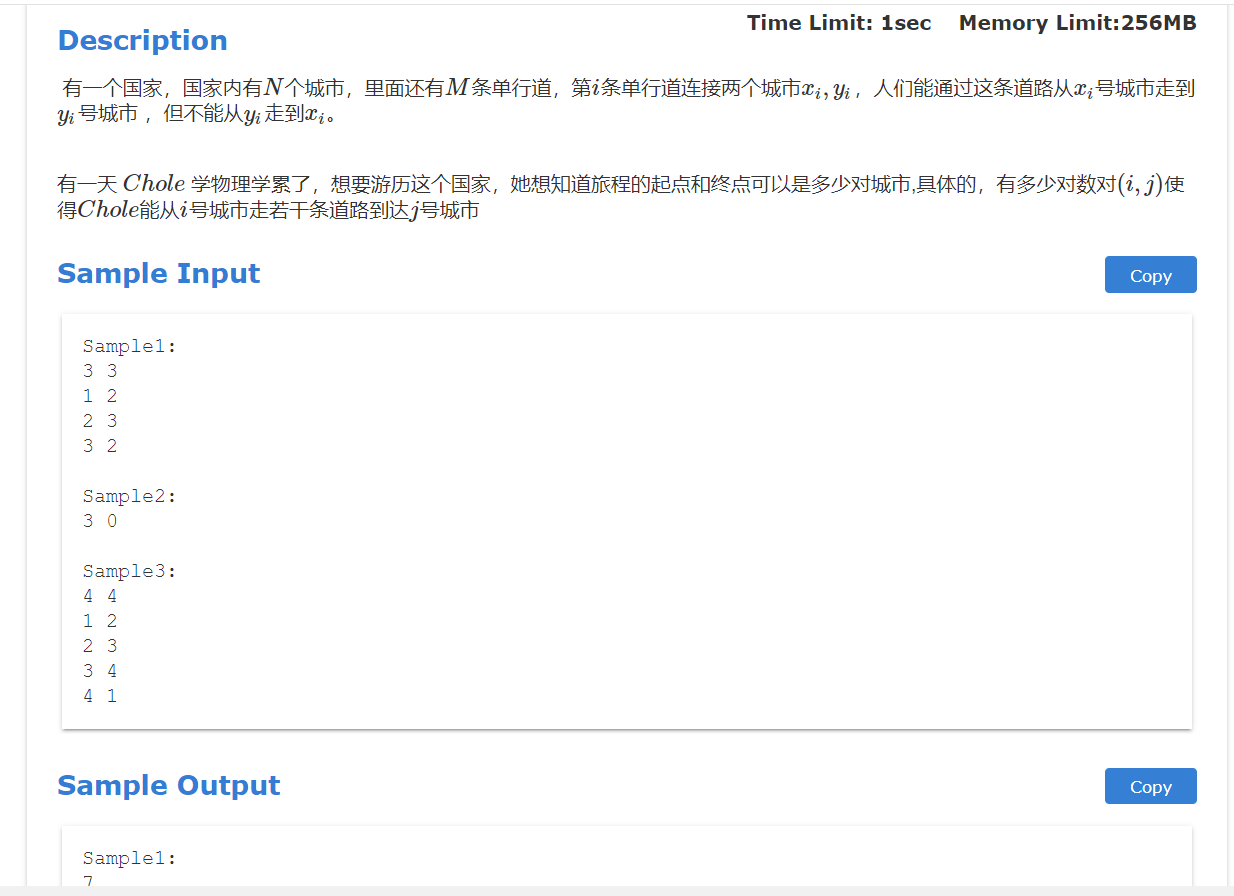
ACMM周赛第一场 T4

题目

image-20240515173905910

思路

对每一个点都进行dfs，复杂度应该在$O(n^2)$左右，如果用warshall算法复杂度为$O(n^3)$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <vector>

using namespace std;
#define N 20005
vector<int> g[N];
int ans = 0;
void dfs(int node,vector<int>& visited){
    if(visited[node] == 1){
        return;
    }
    visited[node] = 1;
    ans++;
    for(auto x:g[node]){
        dfs(x,visited);
    }
}
int main() {
    // 示例图
    int n,m;
    cin>>n>>m;
    for(int i = 0;i<m;i++){
        int x,y;
        cin>>x>>y;
        g[x].push_back(y);
    }
    for(int i = 1;i<=n;i++){
        vector<int> visited(n+1,0);
        dfs(i,visited);
    }
    cout<<ans;
    return 0;
}

ACMM周赛第二场 T3

题目

image-20240520200742230

思路

此题是0-1背包和完全背包的结合，在此记录一下0-1背包和完全背包模板

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;
#define int long long
int dp[10005] = {0};
signed main(){
    int n,m;
    cin>>n>>m;
    for(int i = 0;i<m;i++){
        int x,y,z;
        cin>>x>>y>>z;
        if(z == 1){
            for(int i = n;i>=x;i--){
                dp[i] = max(dp[i],dp[i-x]+y);
            }
        }else{
            for(int i = x;i<=n;i++){
                dp[i] = max(dp[i],dp[i-x]+y);
            }
        }
    }
    cout<<dp[n];
}

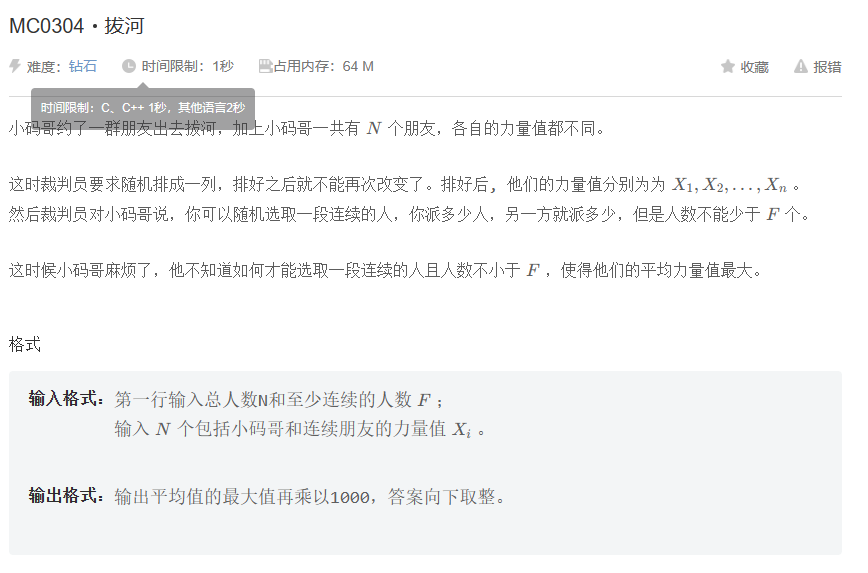
MC0304拔河

题目

image-20240619092350618

思路

题目可以简化为求平均值最大的连续子数组，并且要求子数组长度大于F。

涉及到连续子数组的平均值，可以想到连续子数组的和，而利用两个前缀和的差可以很好的求连续子数组的和。

很明显这个最大平均值大于等于数组的最小值，也小于等于数组的最大值，所以我们可以用二分法来不断逼近这个平均值，假设mid为平均值，那么此时如果有连续数组的和（此时的数组的每个元素已经减去mid）大于0，则说明这个平均值小了，此时令left = mid，继续循环即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<bits/stdc++.h>
using namespace std;
double nums[1000001];
int n,f;
bool check(double mid){
    double b[n+5];
    double y = 0;
    for(int i = 0;i<n;i++){
        if(i > 0){
            b[i] = b[i-1]-mid+nums[i];
        }
        else{
            b[i] = nums[i] - mid;
        }
        if(i >= f-1){
            if(i == f-1){
                if(b[i] > 0){
                    return true;
                }
            
            }
            else{
                y = min(y,b[i-f]);
                if(b[i] - y >= 0){
                    return true;
                }
            }
        }
    }
    return false;
}
int main(){
    cin>>n>>f;
    double l = 3000;
    double r = 0;
    for(int i=0;i<n;i++){
        cin>>nums[i];
        l = min(l,nums[i]);
        r = max(r,nums[i]);
    }
    double left = l;
    double right = r;
    double mid;
    while(right - left >= 1e-6){
        mid = (right+left)/2;
        if(check(mid)){
            left = mid;
        }
        else{
            right = mid;
        }
    }
    //cout<<(int)(mid*1000)<<endl;
    int ans = right*1000;
    cout<<ans;

}

MC0357

题目

image-20240624130853525

思路

阶乘可以提前用一个数组提前算好并保存，使得每次测试都可以使用

求逆元要用费马小定理，即若(a,p) =1，则$a^{p-1}\equiv1modp$，那么a的逆元就可以用$a^{p-2}$​求出，此题也可以先求出100的逆元之后不断重复使用

求一个数的幂也可以使用不断的平方来快速求出幂

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<bits/stdc++.h> 
#define int long long
using namespace std;
const int mod = 998244353;
const int N = 3e5+7;
int f[N];
int binpow(int a,int b){
    int ans = 1;
    while(b >0){
        if(b &1){
            ans = ans*a% mod;
        }
        a = a*a%mod;
        b /= 2;
    }
    return ans;

}
signed main( )
{
    int t;
    cin>>t;
    f[0] = 1;
    for(int i =1;i<=N;i++){
        f[i] = f[i-1]*i%mod;
    }
    while(t--){
        int x1,y1,x2,y2,n,p,q;
        cin>>x1>>y1>>x2>>y2>>n>>p>>q;
        if(x2 - x1>=0 && y2-y1>=0 && x2+y2-x1-y1 == n){
            p = p*binpow(100,mod-2)%mod;
            q = q*binpow(100,mod-2)%mod;
            int ans = (f[n]*binpow(f[n-(x2-x1)]*f[x2-x1]%mod,mod-2))%mod*binpow(p,x2-x1)%mod*binpow(q,y2-y1)%mod;
            cout<<ans<<endl;

        }
        else{
            cout<<0<<endl;
        }
    }
    return 0;
}

mc0361

题目

image-20240728234906320

思路

离线反向并查集+启发式合并

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+5;
const int M = 4e5+5;
struct edge{
    int x,y;
}edges[M];
struct op{
    int opc,x,y;
}ops[M];
map<int,int> st[N];
int fa[N];
int vis[M];
int a[N];
int ans[N];
int find(int x){
    return x == fa[x]?x:find(fa[x]);
}
void merge(int x,int y){
    int u = find(x);
    int v = find(y);
    if(u == v){
        return;
    }
    if(st[u].size() > st[v].size()){
        swap(u,v);
    }
    for(auto t:st[u]){
        st[v][t.first] += t.second;
    }
    st[u].clear();
    fa[u] = v;
}
signed main(){
    int n,m,q;
    cin>>n>>m>>q;
    memset(vis,0,sizeof(int)*M);
    for(int i = 1;i<=n;i++){
        cin>>a[i];
        fa[i] = i;
        st[i][a[i]] = 1;
    }
    for(int i = 1;i<=m;i++){
        cin>>edges[i].x>>edges[i].y;
    }
    for(int i = 1;i<=q;i++){
        cin>>ops[i].opc>>ops[i].x;
        if(ops[i].opc == 2){
            cin>>ops[i].y;
        }
        else{
            vis[ops[i].x] = 1;
        }
    }
    for(int i = 1;i<=m;i++){
        if(vis[i] == 0){
            merge(edges[i].x,edges[i].y);
        }
    }
    for(int i =q;i>=1;i--){
        if(ops[i].opc == 1){
            merge(edges[ops[i].x].x,edges[ops[i].x].y);
        }
        else{
            ans[i] = st[find(ops[i].x)][ops[i].y -a[ops[i].x]];
            if(a[ops[i].x] == ops[i].y - a[ops[i].x]){
                ans[i]--;
            }
        }
    }
    for(int i = 1;i<= q;i++){
        if(ops[i].opc == 2)
        cout<<ans[i]<<endl;
    }
}