doovvv
0%

二叉平衡树

Posted on Edited on Valine:

AVL Tree

Definition

二叉平衡树为一颗空树，或者满足以下两个性质：
* 左子树和右子树的深度之差不大于1 * 左子树和右子树都是平衡二叉树

与普通的搜索二叉树的结构类似，代码如下：

1
2
3
4
5
class Node{
    public:
    int data,height;
    Node *left,*right;
};
平衡因子：左子树深度减去右子树深度,所以平衡二叉树要求每个节点的平衡因子绝对值小于等于1
代码如下：
1
2
3
int getBanlanceFactor(Node* root){
    return getHeight(root->left)-getHeight(root->right);
}

Function

与普通的搜索二叉树相同，主要利用递归。
代码如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void search(Node* root,int v){
    if(root == nullptr){
        return;
    }
    if(root->data == v){
        std::cout<<"Found "<<v<<std::endl;
        return;
    }
    if(v<root->data){
        search(root->left,v);
    }
    else{
        search(root->right,v);
    }
}

insert

与搜索二叉树不同的是，在插入了一个节点之后，二叉树的深度发生了变化，所以某些的节点的平衡因子发生变化，也就不是平衡二叉树了，此时就需要把二叉树进行一定的旋转以得到平衡二叉树。
让我们来看一些需要旋转的情况 #### LL型旋转 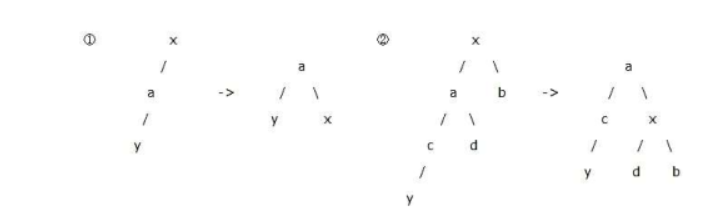如图所示，对于LL型二叉树，根节点的平衡因子为2，此时需要右旋。具体过程为： * 将x的左子树变为它原本左子树a的右子树 * 将a的右子树变为x * 更新x和a的深度，并把a设置为根节点

1
2
3
4
5
6
7
8
void rightRotation(Node*& root){
    Node* temp = root->left;
    root->left = temp->right;
    temp->right = root;
    updateHeight(root);
    updateHeight(temp);
    root = temp;
}

RR型旋转


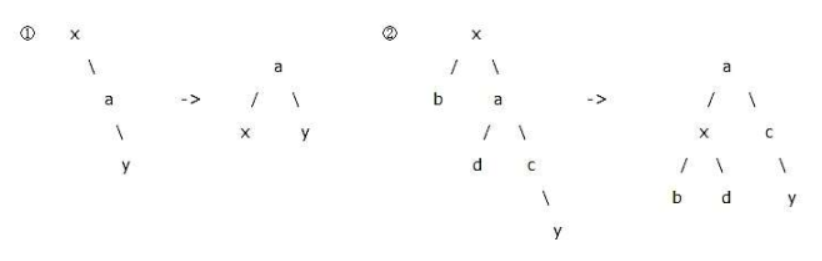
如图所示，对于LL型二叉树，根节点的平衡因子为-2，此时需要左旋。具体过程为： * 将x的左子树变为它原本左子树a的右子树 * 将a的右子树变为x * 更新x和a的深度，并把a设置为根节点